Model de Kuramoto

El model de Kuramoto (o model de Kuramoto-Daido), proposat per primera vegada per Yoshiki Kuramoto (蔵本 由紀, , Kuramoto Yoshiki^?),^[1][2] és un model matemàtic utilitzat per descriure la sincronització. Més concretament, és un model per al comportament d'un gran conjunt d'oscil·ladors acoblats.^[3][4] La seva formulació va estar motivada pel comportament de sistemes d’oscil·ladors químics i biològics, i ha trobat aplicacions generalitzades com en neurociències^[5][6][7][8] i dinàmiques de flames oscil·lants.^[9][10] Kuramoto es va sorprendre molt quan el comportament d'alguns sistemes físics, és a dir, matrius acoblades d'unions de Josephson, va seguir el seu model.^[11]

El model fa diverses suposicions, incloent que hi ha un acoblament feble, que els oscil·ladors són idèntics o gairebé idèntics i que les interaccions depenen sinusoidalment de la diferència de fase entre cada parell d'objectes.

En la versió més popular del model de Kuramoto, es considera que cadascun dels oscil·ladors té la seva pròpia freqüència natural intrínseca ${\displaystyle \omega _{i}}$, i cadascun està acoblat per igual a tots els altres oscil·ladors. Sorprenentment, aquest model completament no lineal es pot resoldre exactament en el límit dels oscil·ladors infinits, N→ ∞;^[5] alternativament, utilitzant arguments d’autoconsistència es poden obtenir solucions en estat estacionari del paràmetre d’ordre.^[12]

La forma més popular del model té les següents equacions governants:

${\displaystyle {\frac {d\theta _{i}}{dt}}=\omega _{i}+{\frac {K}{N}}\sum _{j=1}^{N}\sin(\theta _{j}-\theta _{i}),\qquad i=1\ldots N}$,

on el sistema es compon de N oscil·ladors de cicle-límit, amb fases ${\displaystyle \theta _{i}}$ i constant d'acoblament K.

• 
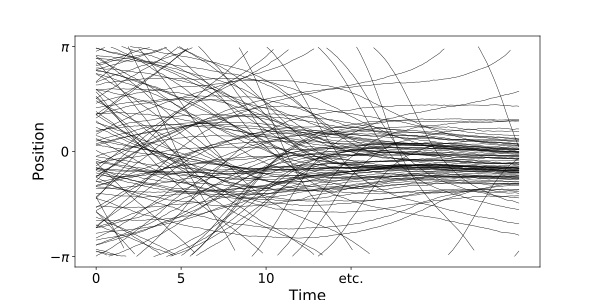  Aquesta imatge descriu la trajectòria de 100 oscil·ladors les fases dels quals es distribueixen inicialment uniformement i amb derivacions dibuixades segons un Gauss amb nul·la mitjana de variància 0'25. El terme d’acoblament és de 0'6. El soroll tèrmic té una intensitat de 0'05. Tot s’integra mitjançant un integrador d’Euler
• Bloqueig de fase en el model de Kuramoto

Es pot afegir soroll al sistema. En aquest cas, l'equació original queda modificada a:

${\displaystyle {\frac {d\theta _{i}}{dt}}=\omega _{i}+\zeta _{i}+{\dfrac {K}{N}}\sum _{j=1}^{N}\sin(\theta _{j}-\theta _{i})}$,

on ${\displaystyle \zeta _{i}}$ és la fluctuació i una funció del temps. Si considerem que el soroll és un soroll blanc, llavors:

${\displaystyle \langle \zeta _{i}(t)\rangle =0}$ ,

${\displaystyle \langle \zeta _{i}(t)\zeta _{j}(t')\rangle =2D\delta _{ij}\delta (t-t')}$

amb ${\displaystyle D}$ que denota la força del soroll.

La transformació que permet resoldre aquest model amb exactitud (almenys en el límit N → ∞) és la següent:

Es defineixen els paràmetres «ordre» r i ψ com a

${\displaystyle re^{i\psi }={\frac {1}{N}}\sum _{j=1}^{N}e^{i\theta _{j}}}$.

Aquí r representa la coherència de fase de la població d’oscil·ladors i ψ indica la fase mitjana. Multiplicant aquesta equació per ${\displaystyle e^{-i\theta _{i}}}$ i només tenint en compte la part imaginària dona:

${\displaystyle {\frac {d\theta _{i}}{dt}}=\omega _{i}+Kr\sin(\psi -\theta _{i})}$.

Per tant, les equacions dels oscil·ladors ja no s’acoblen explícitament; en canvi, els paràmetres d’ordre regeixen el comportament. Normalment es fa una transformació addicional a un quadre rotatiu en què la mitjana estadística de fases de tots els oscil·ladors és nul·la (és a dir, ${\displaystyle \psi =0}$). Finalment, l'equació governant es converteix en:

${\displaystyle {\frac {d\theta _{i}}{dt}}=\omega _{i}-Kr\sin(\theta _{i})}$.

Ara considerem el cas que N tendeix a l'infinit (N→ ∞). Prenem la distribució de les freqüències naturals intrínseques com g(ω) (suposada normalitzada). Aleshores suposem que la densitat dels oscil·ladors en una fase determinada θ, amb freqüència natural ω donada, en el moment t és ${\displaystyle \rho (\theta ,\omega ,t)}$. La normalització ho requereix

${\displaystyle \int _{-\pi }^{\pi }\rho (\theta ,\omega ,t)\,d\theta =1.}$

L’equació de continuïtat per a la densitat de l’oscil·lador serà

${\displaystyle {\frac {\partial \rho }{\partial t}}+{\frac {\partial }{\partial \theta }}[\rho v]=0,}$

on v és la velocitat de deriva dels oscil·ladors donada prenent el límit N→ ∞ en l'equació governant transformada, tal que

${\displaystyle {\frac {\partial \rho }{\partial t}}+{\frac {\partial }{\partial \theta }}[\rho \omega +\rho Kr\sin(\psi -\theta )]=0.}$

Finalment, hem de reescriure la definició dels paràmetres d’ordre per al límit continuum del límit (N→ ∞). ${\displaystyle \theta _{i}}$ s'ha de substituir per la seva mitjana de conjunt (sobretot ${\displaystyle \omega }$) i la suma s'ha de substituir per una integral, per donar

${\displaystyle re^{i\psi }=\int _{-\pi }^{\pi }e^{i\theta }\int _{-\infty }^{\infty }\rho (\theta ,\omega ,t)g(\omega )\,d\omega \,d\theta .}$

L'estat incoherent amb tots els oscil·ladors a la deriva correspon a la solució ${\displaystyle \rho =1/(2\pi )}$. En aquest cas ${\displaystyle r=0}$, i no hi ha coherència entre els oscil·ladors. Es distribueixen uniformement en totes les fases possibles i la població es troba en estat estacionari (tot i que els oscil·ladors individuals continuen canviant de fase d’acord amb la seva ω intrínseca).

Quan l'acoblament K és prou fort, és possible una solució totalment sincronitzada. En estat totalment sincronitzat, tots els oscil·ladors comparteixen una freqüència comuna, tot i que les seves fases poden ser diferents.

Una solució per al cas de la sincronització parcial produeix un estat en què només alguns oscil·ladors (els propers a la freqüència natural mitjana del conjunt) se sincronitzen; altres oscil·ladors deriven de manera incoherent. Matemàticament, l'estat és

${\displaystyle \rho =\delta \left(\theta -\psi -\arcsin \left({\frac {\omega }{Kr}}\right)\right)}$

per a oscil·ladors bloquejats, i

${\displaystyle \rho ={\frac {\rm {constant\;de\;normalitzaci{\acute {o}}}}{(\omega -Kr\sin(\theta -\psi ))}}}$

per a oscil·ladors a la deriva. El tall es produeix quan ${\displaystyle |\omega |<Kr}$.

El model dissipatiu de Kuramoto es troba en certs sistemes hamiltonians conservadors^[13] amb hamiltonians de la forma:

${\displaystyle {\mathcal {H}}(q_{1},\ldots ,q_{N},p_{1},\ldots ,p_{N})=\sum _{i=1}^{N}{\frac {\omega _{i}}{2}}(q_{i}^{2}+p_{i}^{2})+{\frac {K}{4N}}\sum _{i,j=1}^{N}(q_{i}p_{j}-q_{j}p_{i})(q_{j}^{2}+p_{j}^{2}-q_{i}^{2}-p_{i}^{2})}$

Després d’una transformació canònica a variables d’angle d’acció amb accions ${\displaystyle I_{i}=\left(q_{i}^{2}+p_{i}^{2}\right)/2}$ i angles (fases) ${\displaystyle \phi _{i}=\mathrm {arctan2} \left(q_{i}/p_{i}\right)}$, la dinàmica exacta de Kuramoto sorgeix en múltiples varietats invariants de constant ${\displaystyle I_{i}\equiv I}$. Amb el hamiltonià transformat:

${\displaystyle {\mathcal {H'}}(I_{1},\ldots I_{N},\phi _{1}\ldots ,\phi _{N})=\sum _{i=1}^{N}\omega _{i}I_{i}-{\frac {K}{N}}\sum _{i=1}^{N}\sum _{j=1}^{N}{\sqrt {I_{j}I_{i}}}(I_{j}-I_{i})\sin(\phi _{j}-\phi _{i}),}$

L'equació de moviment de Hamilton es converteix en:

${\displaystyle {\frac {dI_{i}}{dt}}=-{\frac {\partial {\mathcal {H}}'}{\partial \phi _{i}}}=-{\frac {2K}{N}}\sum _{k=1}^{N}{\sqrt {I_{k}I_{i}}}(I_{k}-I_{i})\cos(\phi _{k}-\phi _{i})}$

i

${\displaystyle {\frac {d\phi _{i}}{dt}}={\frac {\partial {\mathcal {H}}'}{\partial I_{i}}}=\omega _{i}+{\frac {K}{N}}\sum _{k=1}^{N}\left[2{\sqrt {I_{i}I_{k}}}\sin(\phi _{k}-\phi _{i})\right.\left.+{\sqrt {I_{k}/I_{i}}}(I_{k}-I_{i})\sin(\phi _{k}-\phi _{i})\right].}$

Així que la varietat amb ${\displaystyle I_{j}=I}$ és invariant perquè ${\displaystyle {\frac {dI_{i}}{dt}}=0}$ i la dinàmica de fases ${\displaystyle {\frac {d\phi _{i}}{dt}}}$ es converteix en la dinàmica del model de Kuramoto (amb les mateixes constants d'acoblament per a ${\displaystyle I=1/2}$). La classe dels sistemes hamiltonians caracteritza certs sistemes quàntics-clàssics, inclosos els condensats de Bose-Einstein.

Hi ha una sèrie de tipus de variacions que es poden aplicar al model original presentat anteriorment. Alguns models canvien d’estructura topològica, d’altres permeten pesos heterogenis i altres canvis estan més relacionats amb models inspirats en el model de Kuramoto però que no tenen la mateixa forma funcional.

• 
  Patrons de sincronització diferents en una matriu bidimensional d’oscil·ladors semblants a Kuramoto amb diferents funcions d’interacció de fase i topologies d’acoblament espacial. (A) Molinets. (B) Onades. (C) Quimeres. (D) Quimeres i ones combinades. L'escala de colors indica la fase de l’oscil·lador
• Els metrònoms, inicialment desfasats, se sincronitzen mitjançant petits moviments de la base sobre la qual es col·loquen. Aquest sistema ha demostrat ser equivalent al model de Kuramoto.^[14]

A més del model original, que té una topologia global, una topologia prou densa i semblant a la xarxa complexa és susceptible del tractament de camp mitjà utilitzat en la solució del model original^[15] (vegeu els apartats Transformació i Límit N→ ∞ anteriors per obtenir més informació). Topologies de xarxes com ara anells i poblacions acoblades donen suport als estats quimera.^[16] També es pot demanar el comportament de models en què hi ha intrínsecament locals, com ara topologies unidimensionals que la cadena i l'anell són exemples prototípics. En aquestes topologies, en què l'acoblament no és escalable segons amb 1/N, no és possible aplicar l'enfocament canònic del camp mitjà, de manera que cal confiar en l'anàlisi cas per cas, fent ús de simetries sempre que sigui possible, que pot donar base a l'abstracció dels principis generals de les solucions.

Es poden observar sincronies uniformes, ones i espirals fàcilment en xarxes de Kuramoto bidimensionals amb acoblament local difusiu. L'estabilitat de les ones en aquests models es pot determinar analíticament mitjançant els mètodes d’anàlisi d’estabilitat de Turing.^[17] La sincronia uniforme tendeix a ser estable quan l'acoblament local és positiu a tot arreu, mentre que les ones sorgeixen quan les connexions de llarg abast són negatives (acoblament envoltant inhibitori). Les ones i la sincronia estan connectades per una branca de solucions topològicament diferent coneguda com a ondulació.^[18] Es tracta de desviacions espacialment periòdiques de baixa amplitud que emergeixen de l'estat uniforme (o l'estat d'ona) mitjançant una bifurcació de Hopf.^[19] Wiley, Strogatz i Girvan^[20] van predir (però no van observar) l'existència de solucions d'ondulació, que els van anomenar estats q multi-retorçats.

La topologia sobre la qual s’estudia el model de Kuramoto es pot fer adaptativa mitjançant l’ús d’un model de fitness que mostra la millora de la sincronització i la percolació d’una manera autoorganitzada.^[21]

Alguns treballs a la comunitat de control s’han centrat en el model de Kuramoto en xarxes i amb pesos heterogenis (és a dir, la força d’interconnexió entre dos oscil·ladors qualsevol pot ser arbitrària). La dinàmica d’aquest model és la següent:

${\displaystyle {\frac {d\theta _{i}}{dt}}=\omega _{i}+\sum _{j=1}^{N}a_{ij}\sin(\theta _{j}-\theta _{i}),\qquad i=1\ldots N}$

on ${\displaystyle a_{ij}}$ és un nombre real positiu diferent de zero si l'oscil·lador ${\displaystyle j}$ està connectat a l'oscil·lador ${\displaystyle i}$. Aquest model permet un estudi més realista de, per exemple, el flocatge, l'escolarització i el vehicle de coordinació.^[22] En el treball de Dörfler i col·legues, diversos teoremes proporcionen condicions rigoroses per a la sincronització de fase i freqüència d’aquest model. Altres estudis, motivats per observacions experimentals en neurociències, se centren a derivar condicions analítiques per a la sincronització de clústers d’oscil·ladors de Kuramoto heterogenis en topologies arbitràries de xarxa.^[23] Atès que el model de Kuramoto sembla tenir un paper clau en l'avaluació dels fenòmens de sincronització al cervell,^[24] les condicions teòriques que donen suport a les troballes empíriques poden obrir el camí per a una comprensió més profunda dels fenòmens de sincronització neuronal.

Kuramoto va aproximar la interacció de fase entre dos oscil·ladors qualsevol pel seu primer component de Fourier, és a dir ${\displaystyle \Gamma (\phi )=\sin(\phi )}$,on ${\displaystyle \phi =\theta _{j}-\theta _{i}}$. Es poden obtenir millors aproximacions incloent components de Fourier d’ordre superior,

${\displaystyle \Gamma (\phi )=\sin(\phi )+a_{1}\sin(2\phi +b_{1})+...+a_{n}\sin(2n\phi +b_{n})}$,

on els paràmetres ${\displaystyle a_{i}}$ i ${\displaystyle b_{i}}$ s’han d’estimar. Per exemple, la sincronització entre una xarxa de neurones de Hodgkin-Huxley dèbilment acoblades es pot replicar mitjançant oscil·ladors acoblats que conserven els primers quatre components de Fourier de la funció d'interacció.^[25] La introducció de termes d’interacció de fase d’ordre superior també pot induir fenòmens dinàmics interessants com estats parcialment sincronitzats,^[26] cicles heteroclínics,^[27] i dinàmiques caòtiques.^[28]

• La biblioteca pyclustering inclou una implementació de Python i C++ del model de Kuramoto i les seves modificacions. La biblioteca també consta de xarxes oscil·latòries (per a l'anàlisi de clústers, reconeixement de patrons, coloració de gràfics, segmentació d'imatges) que es basen en el model de Kuramoto i l'oscil·lador de fase.^[29]

• Funció mestra d'estabilitat
• Xarxa neuronal oscil·latòria