Stavový popis systému

Stavový popis systému se používá pro systémy s více vstupy a výstupy, tzv. MIMO systémy. Používá se maticový zápis. Tento článek se zabývá stavovým popisem systému, který vzejde z linearizace typicky nelineárních diferenciálních rovnic v okolí takzvaného pracovního bodu, který bývá ekvilibriem. Poté stavový popis dobře popisuje chování systému jen v okolí tohoto pracovního bodu lineární aproximací, což se dá použít pro lineární řízení.

• Stav systému - Je to nejmenší počet stavových proměnných, určuje ho stavový vektor
• Stavový vektor - Jde o sloupcový vektor často značený ${\displaystyle \mathbf {x} (t)}$, jehož složky tvoří stavové proměnné
• Stavové proměnné - Jde o časové funkce, které určují stav dynamického systému
• Stavový prostor - ${\displaystyle n}$-rozměrný prostor reálných čísel ${\displaystyle {\mathcal {R}}^{n}}$
• Vektor vstupů - Jde o sloupcový vektor ${\displaystyle \mathbf {u} (t)}$
• Vektor výstupů - Jde o sloupcový vektor ${\displaystyle \mathbf {y} (t)}$
• Stavové rovnice - Určují vazbu mezi stavem a vstupy a výstupy systému. Jsou dvě, zde popsané jsou lineární, časově invariantní.
• Stavová trajektorie - Stav je vektor, jehož poloha se mění a na konci vytváří křivku

Umožňuje vazbu derivace stavové proměnné na libovolný vstup nebo výstup. Rovnice je

${\displaystyle {\frac {d\mathbf {x} (t)}{dt}}=\mathbf {Ax} (t)+\mathbf {Bu} (t)}$

Určuje vztah mezi vektorem výstupu a vektorem vstupu a vektorem stavu

${\displaystyle \mathbf {y} (t)=\mathbf {Cx} (t)+\mathbf {Du} (t)}$

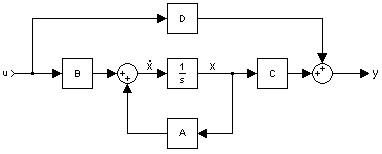
${\displaystyle \mathbf {A} }$ - matice vnitřních vazeb systému (matice systému)

${\displaystyle \mathbf {B} }$ - matice vazeb systému na vstup (matice řízení)

${\displaystyle \mathbf {C} }$ - matice vazeb výstupu na stav

${\displaystyle \mathbf {D} }$ - matice vazeb vstupu na výstup. Z hlediska dynamických vlastností je vliv zanedbatelný a považuje se často za nulový.

Jde o jednoznačný převod, v podstatě se jedná o řešení obou stavových rovnic po provedení Laplaceovy transformace. Matice ${\displaystyle \mathbf {A} }$, ${\displaystyle \mathbf {B} }$, ${\displaystyle \mathbf {C} }$ a ${\displaystyle \mathbf {D} }$ jsou známé. Matice ${\displaystyle \mathbf {I} \in {\mathcal {R}}^{n\times n}}$ je jednotková matice. Řešením je rovnice

${\displaystyle \mathbf {G} (s)={\frac {\mathbf {Y} (s)}{\mathbf {U} (s)}}=\mathbf {C} {(s\mathbf {I} -\mathbf {A} )}^{-1}\mathbf {B} +\mathbf {D} =\mathbf {C} {\frac {1}{\mathrm {det} {(s\mathbf {I} -\mathbf {A} )}}}{\mathrm {adj} {(s\mathbf {I} -\mathbf {A} )}}\mathbf {B} +\mathbf {D} }$.

Výraz ${\displaystyle \mathrm {det} (s\mathbf {I} -\mathbf {A} )}$ nazveme charakteristickým polynomem systému a kořeny tohoto polynomu nazveme póly systému. Poloha těchto pólů v komplexní rovině určuje stabilitu systému (leží-li alespoň jeden pól napravo od imaginární osy, je systém nestabilní).

Převod není jednoznačný používají se tři algoritmy

• Přímé programování
• Paralelní programování
• Sériové programování

• I.Švarc, M.Šeda, M.Vítečková. Automatické řízení
• P.Blaha, P.Vavřín. Řízení a regulace 1. Skriptum VUT