Kantenzahl

Als Kantenzahl bezeichnet man in der Graphentheorie die Anzahl der Kanten eines Graphen.

Ist ${\displaystyle G}$ der betrachtete Graph, so notiert man diese Zahl in der Regel mit ${\displaystyle m(G)}$ (oder kurz ${\displaystyle m}$, falls klar ist, um welchen Graph es sich handelt). Alternativ schreibt man auch ${\displaystyle ||G||}$.

Bei ungerichteten Graphen ist die Kantenzahl ${\displaystyle m(G)}$ eines gegebenen Graphen ${\displaystyle G=(V,E)}$ die Anzahl seiner Kanten, bzw. die Summe der Vielfachheiten der einzelnen Kanten, wenn es sich um einen Graphen mit Mehrfachkanten handelt.

Man kann sie auch als Mächtigkeit ${\displaystyle |E|}$ der Kantenmenge ${\displaystyle E}$ sehen.

• Es gilt: ${\displaystyle m(G)\geq \Delta _{\tau (G)-1}={\frac {\tau (G)(\tau (G)-1)}{2}}}$. Dabei ist ${\displaystyle \tau (G)}$ die Cliquenzahl von ${\displaystyle G}$; die Anzahl der Knoten in der größten Clique von ${\displaystyle G}$. Gleichheit tritt bei vollständigen Graphen ein.
• Außerdem gilt

${\displaystyle m(G)\geq \sum _{v\in U}d(v)}$.
${\displaystyle U}$ ist dabei eine stabile Menge von ${\displaystyle G}$ und ${\displaystyle d(v)}$ der Grad des Knoten ${\displaystyle v}$. Tritt Gleichheit ein, so ist ${\displaystyle U}$ eine maximale stabile Menge des Graphen ${\displaystyle G}$.

Ist die Adjazenzmatrix eines Graphen gegeben, kann man daraus sehr leicht die Kantenzahl dieses Graphen bestimmen.

Eine Adjazenzmatrix besitzt für eine Kante, die die Knoten ${\displaystyle i}$ und ${\displaystyle j}$ verbindet, einen Eintrag in der ${\displaystyle i}$-ten Zeile und der ${\displaystyle j}$-ten Spalte. Ist der Graph ungerichtet, steht die 1 auch in der ${\displaystyle j}$-ten Zeile und der ${\displaystyle i}$-ten Spalte.

Um die Kantenzahl zu berechnen, muss man nur alle Einträge addieren und noch durch 2 teilen. Dieses Verfahren funktioniert auch für Graphen mit Mehrfachkanten.

Im folgenden Abschnitt wird immer von einfachen Graphen ausgegangen, also ungerichteten Graphen ohne Mehrfachkanten.

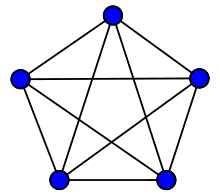
Die Kantenzahl ${\displaystyle m}$ des vollständigen Graphen mit ${\displaystyle n}$ Knoten ${\displaystyle K_{n}}$ entspricht

${\displaystyle m={n \choose 2}={\frac {n(n-1)}{2}}=\Delta _{n-1}}$,

also der Dreieckszahl ${\displaystyle \Delta _{n-1}}$.

Das ist daran zu sehen, dass jede Kante durch zwei Knoten definiert wird und es ${\displaystyle {n \choose 2}}$ Möglichkeiten gibt zwei Knoten auszuwählen.

Bäume mit ${\displaystyle n}$ Knoten haben nach der Cayley-Formel ${\displaystyle m=n-1}$ Kanten. Sie ist ein Sonderfall des Eulerschen Polyedersatzes für planare Graphen (vgl. planare Graphen). Zu der Graphenklasse der Bäume zählen auch lineare Graphen und Sterngraphen. Ein Sterngraph ist ein Graph, der einen zentralen Knoten besitzt, der mit allen anderen Knoten verbunden ist. Die anderen Knoten besitzen nur diesen einen Nachbarn.

Die Kantenzahl eines planaren Graphen lässt sich berechnen mithilfe des Eulerschen Polyedersatzes für planare Graphen

${\displaystyle n-m+l=2}$.

Dabei gilt ${\displaystyle n=|V|,m=|E|}$ und ${\displaystyle l}$ ist die Gebietszahl.

Löst man die Gleichung nach ${\displaystyle m}$ auf, erhält man

${\displaystyle m=n+l-2}$.

Ein maximal planarer Graph ist ein Graph, dem keine weiteren Kanten hinzugefügt werden können. Besitzt er mindestens 3 Knoten, so ist er ein Dreiecksgraph und jedes seiner Gebiete ist von 3 Kanten umgeben.

Die Kantenzahl eines maximalen planaren Graphen mit mindestens 3 Knoten ist ${\displaystyle m=3n-6}$.

Bei einem regulären Graphen mit Grad ${\displaystyle k}$ und ${\displaystyle n}$ Knoten ist die Kantenzahl

${\displaystyle m={\frac {n\cdot k}{2}}}$.

Das kommt daher, dass von jedem Knoten ${\displaystyle k}$ Kanten ausgehen; dabei zählt man allerdings jede Kante zweimal und muss deshalb durch 2 teilen.

Bei gegebenem Durchschnittsgrad ${\displaystyle d(G)}$ und Knotenzahl ${\displaystyle n}$ kann man die Kantenzahl folgendermaßen berechnen

${\displaystyle m={\frac {d(G)\cdot n(G)}{2}}}$.

Durch die Multiplikation mit ${\displaystyle n}$ steht im Zähler die Anzahl aller Kanten; dabei ist allerdings jede doppelt gezählt, deshalb wird noch durch 2 geteilt.

Diese Formel ist eine Verallgemeinerung der Formel für reguläre Graphen.

Handelt es sich bei einem gegebenen Graphen ${\displaystyle G}$ um einen bipartiten Graphen, dessen Knotenmenge ${\displaystyle V}$ sich in zwei disjunkte Teilmengen ${\displaystyle V_{1}}$ und ${\displaystyle V_{2}}$ aufteilen lässt, dann lässt sich nur ein Maximum für die Kantenzahl angeben.

Jeder Knoten ${\displaystyle v\in V_{1}}$ kann mit maximal ${\displaystyle |V_{2}|}$ verschiedenen Knoten ${\displaystyle w\in V_{2}}$ durch eine Kante verbunden sein.

Also gibt es maximal ${\displaystyle m=|V_{1}|\cdot |V_{2}|}$ Kanten.

Ist ${\displaystyle G}$ ein vollständig bipartiter Graph, dann ist die Kantenzahl maximal und erreicht genau ${\displaystyle |V_{1}|\cdot |V_{2}|}$.

Allgemein beträgt die maximale Kantenzahl eines k-partiten Graphen ${\displaystyle G=(V,E)}$ mit den ${\displaystyle k}$ disjunkten Teilmengen ${\displaystyle V_{1},\dotsc ,V_{k}}$

${\displaystyle {\begin{aligned}m&=\Delta _{|V|-1}-\Delta _{|V_{1}|-1}-\dotsb -\Delta _{|V_{k}|-1}\\&=\left({\frac {|V|(|V|-1)}{2}}\right)-\left({\frac {|V_{1}|(|V_{1}|-1)}{2}}\right)-\left({\frac {|V_{2}|(|V_{2}|-1)}{2}}\right)-\dotsb -\left({\frac {|V_{k}|(|V_{k}|-1)}{2}}\right)\\&={\frac {(|V|^{2}-|V|)-(|V_{1}|^{2}-|V_{1}|)-(|V_{2}|^{2}-|V_{2}|)-\dotsb -(|V_{k}|^{2}-|V_{k}|)}{2}}\\&={\frac {|V|^{2}-|V|-|V_{1}|^{2}+|V_{1}|-|V_{2}|^{2}+|V_{2}|-\dotsb -|V_{k}|^{2}+|V_{k}|}{2}}\\&={\frac {|V|^{2}-|V_{1}|^{2}-|V_{2}|^{2}-\dotsb -|V_{k}|^{2}-|V|+|V_{1}|+|V_{2}|+\dotsb +|V_{k}|}{2}}\\&={\frac {|V|^{2}-|V_{1}|^{2}-|V_{2}|^{2}-\dotsb -|V_{k}|^{2}}{2}}\end{aligned}}}$

Dabei steht ${\displaystyle \Delta _{k}}$ für die ${\displaystyle k}$-te Dreieckszahl. Die Formel kann man herleiten, indem man überlegt, wie viele Kanten zu einem vollständigen Graphen noch fehlen.

Da jeder ${\displaystyle k}$-knotenfärbbare Graph auch ${\displaystyle k}$-partit ist, kann man bei ${\displaystyle k}$-knotenfärbbaren Graphen auch die oben genannte Formel anwenden.

Ein Gittergraph ${\displaystyle G_{i,j}}$ mit ${\displaystyle n=i\cdot j}$ Knoten lässt sich als Rechteck darstellen, in dem alle Kanten die gleiche Länge haben.

Die Kantenzahl kann man berechnen, indem man erst die äußeren Kanten zählt und dann die inneren addiert.

Es gibt

${\displaystyle {\begin{aligned}m_{1}&=(2i-2)+(2j-2)\\&=2i+2j-4\end{aligned}}}$

äußere Kanten und

${\displaystyle {\begin{aligned}m_{2}&=[(i-2)(j-1)]+[(i-1)(j-2)]\\&=i\cdot j-i-2j+2+i\cdot j-j-2i+2\\&=2ij-3i-3j+4\end{aligned}}}$

innere Kanten. Zusammen ergibt das

${\displaystyle {\begin{aligned}m&=m_{1}+m_{2}\\&=(2i+2j-4)+(2ij-3i-3j+4)\\&=2ij-i-j\end{aligned}}}$

Kanten.

Alternativ kann man die Anzahl der senkrechten und die Anzahl der waagerechten Kanten addieren und erhält

${\displaystyle {\begin{aligned}(i-1)\cdot j+(j-1)\cdot i=2ij-i-j\end{aligned}}}$

Kanten.

Ein Leitergraph besitzt die Struktur einer Leiter. Er besteht aus zwei linearen Graphen gleicher Länge (die Holme), wobei je zwei einander entsprechende Knoten durch eine Kante (die Sprossen) miteinander verbunden sind.

Der Leitergraph ${\displaystyle L_{n}}$ mit ${\displaystyle 2n}$ Knoten besitzt ${\displaystyle 2n-2}$ Kanten für die Holme und ${\displaystyle n}$ Kanten für die Sprossen, also insgesamt

${\displaystyle m=2n-2+n=3n-2}$

Kanten.

Ein Radgraph besteht aus einem Kreisgraph ${\displaystyle C_{n}}$, dem ein weiterer mit allen Knoten verbundener Knoten hinzugefügt wurde. Der Radgraph ${\displaystyle W_{n}}$ besitzt ${\displaystyle n+1}$ Knoten.

Die Kantenzahl von ${\displaystyle W_{n}}$ berechnet sich durch

${\displaystyle w=2n}$.

Zu einem gegebenen Graphen ${\displaystyle G=(V,E)}$ entsteht der duale Graph ${\displaystyle G'=(V',E')}$, indem jedes Gebiet von ${\displaystyle G}$ durch einen Knoten von ${\displaystyle G'}$ ersetzt wird. Außerdem werden Kanten, die Gebiete von ${\displaystyle G}$ trennten, zu Kanten, die die neuen Knoten von ${\displaystyle G'}$ verbinden.

Die Kantenzahl bleibt bei diesem Verfahren gleich, also gilt

${\displaystyle m(G)=m(G')}$.

Dass zwei Graphen isomorph zueinander sind, bedeutet, dass sie strukturell gleich sind und sich nur in der Bezeichnung der Knoten und Kanten unterscheiden.

Deshalb gilt für zwei zueinander isomorphe Graphen ${\displaystyle G}$ und ${\displaystyle G'}$

${\displaystyle m(G)=m(G')}$.

Der Komplementgraph eines Graphen ${\displaystyle G=(V,E)}$ ist der Graph ${\displaystyle G'=(V',E')}$, der die gleiche Knotenmenge ${\displaystyle V'}$ wie ${\displaystyle G}$ besitzt, aber alle Kanten, die ${\displaystyle G}$ nicht hat.

Die Kantenzahl des Komplementgraphen von ${\displaystyle G}$ kann abhängig von der Kantenzahl von ${\displaystyle G}$ berechnet werden.

${\displaystyle {\begin{aligned}m(G')&=\Delta _{n(G)-1}-m(G)\\&={\frac {n(G)(n(G)-1)}{2}}-m(G)\end{aligned}}}$

Dabei steht ${\displaystyle n(G)}$ für die Knotenzahl von ${\displaystyle G}$. Die Formel leitet sich her, da die Vereinigungsmenge der beiden Knotenmengen einen vollständigen Graph bildet.

Der Kantengraph ${\displaystyle L(G)=(V',E')}$ eines Graphen ${\displaystyle G=(V,E)}$ entsteht, indem jede Kante von ${\displaystyle G}$ zu einem Knoten von ${\displaystyle L(G)}$ wird. Dann werden die Knoten von ${\displaystyle L(G)}$ durch eine Kante verbunden, die in ${\displaystyle G}$ benachbart waren.

Die Formel für die Kantenzahl von ${\displaystyle L(G)}$ lässt sich herleiten durch die Überlegung, dass jeder Knoten ${\displaystyle v\in V}$ von ${\displaystyle G}$ ersetzt wird durch ${\displaystyle {\tbinom {d(v)}{2}}=\Delta _{d(v)-1}}$ Kanten, die die an Stelle der angrenzenden Kanten entstandenen Knoten verbinden.

Also lautet sie

${\displaystyle m(L(G))=\sum _{v\in V}{\binom {d(v)}{2}}=\sum _{v\in V}\Delta _{d(v)-1}}$.

• Knotenzahl
• Kante (Graphentheorie)