Graph product

In graph theory, a graph product is a binary operation on graphs. Specifically, it is an operation that takes two graphs G₁ and G₂ and produces a graph H with the following properties:

• The vertex set of H is the Cartesian product V(G₁) × V(G₂), where V(G₁) and V(G₂) are the vertex sets of G₁ and G₂, respectively.
• Two vertices (a₁,a₂) and (b₁,b₂) of H are connected by an edge, iff a condition about a₁, b₁ in G₁ and a₂, b₂ in G₂ is fulfilled.

The graph products differ in what exactly this condition is. It is always about whether or not the vertices a_n, b_n in G_n are equal or connected by an edge.

The terminology and notation for specific graph products in the literature varies quite a lot; even if the following may be considered somewhat standard, readers are advised to check what definition a particular author uses for a graph product, especially in older texts.

Even for more standard definitions, it is not always consistent in the literature how to handle self-loops. The formulas below for the number of edges in a product also may fail when including self-loops. For example, the tensor product of a single vertex self-loop with itself is another single vertex self-loop with ${\displaystyle E=1}$, and not ${\displaystyle E=2}$ as the formula ${\displaystyle E_{G\times H}=2E_{G}E_{H}}$ would suggest.

The following table shows the most common graph products, with ${\displaystyle \sim }$ denoting "is connected by an edge to", and ${\displaystyle \not \sim }$ denoting non-adjacency. While ${\displaystyle \not \sim }$ does allow equality, ${\displaystyle \not \simeq }$ means they must be distinct and non-adjacent. The operator symbols listed here are by no means standard, especially in older papers.

Name	Condition for ${\displaystyle (a_{1},a_{2})\sim (b_{1},b_{2})}$		Number of edges ${\displaystyle {\begin{array}{cc}v_{1}=\vert \mathrm {V} (G_{1})\vert &v_{2}=\vert \mathrm {V} (G_{2})\vert \\e_{1}=\vert \mathrm {E} (G_{1})\vert &e_{2}=\vert \mathrm {E} (G_{2})\vert \end{array}}}$	Example
		with ${\displaystyle a_{n}~{\text{rel}}~b_{n}}$ abbreviated as ${\displaystyle {\text{rel}}_{n}}$
Cartesian product (box product) ${\displaystyle G_{1}\square G_{2}}$	${\displaystyle a_{1}=b_{1}~\land ~a_{2}\sim b_{2}}$ ${\displaystyle \lor }$ ${\displaystyle a_{1}\sim b_{1}~\land ~a_{2}=b_{2}}$	${\displaystyle =_{1}~\sim _{2}}$ ${\displaystyle \lor }$ ${\displaystyle \sim _{1}~=_{2}}$	${\displaystyle v_{1}~e_{2}~+~e_{1}~v_{2}}$
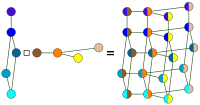Tensor product (Kronecker product, categorical product) ${\displaystyle G_{1}\times G_{2}}$	${\displaystyle a_{1}\sim b_{1}~\land ~a_{2}\sim b_{2}}$	${\displaystyle \sim _{1}~\sim _{2}}$	${\displaystyle 2~e_{1}~e_{2}}$
Lexicographical product ${\displaystyle G_{1}\cdot G_{2}}$ or ${\displaystyle G_{1}[G_{2}]}$	${\displaystyle a_{1}\sim b_{1}}$ ${\displaystyle \lor }$ ${\displaystyle a_{1}=b_{1}~\land ~a_{2}\sim b_{2}}$	${\displaystyle \sim _{1}}$ ${\displaystyle \lor }$ ${\displaystyle =_{1}~\sim _{2}}$	${\displaystyle v_{1}~e_{2}~+~e_{1}~v_{2}^{2}}$
Strong product (Normal product, AND product) ${\displaystyle G_{1}\boxtimes G_{2}}$	${\displaystyle a_{1}=b_{1}~\land ~a_{2}\sim b_{2}}$ ${\displaystyle \lor }$ ${\displaystyle a_{1}\sim b_{1}~\land ~a_{2}=b_{2}}$ ${\displaystyle \lor }$ ${\displaystyle a_{1}\sim b_{1}~\land ~a_{2}\sim b_{2}}$	${\displaystyle =_{1}~\sim _{2}}$ ${\displaystyle \lor }$ ${\displaystyle \sim _{1}~=_{2}}$ ${\displaystyle \lor }$ ${\displaystyle \sim _{1}~\sim _{2}}$	${\displaystyle v_{1}~e_{2}~+~e_{1}~v_{2}~+~2~e_{1}~e_{2}}$
Co-normal product (disjunctive product, OR product) ${\displaystyle G_{1}*G_{2}}$	${\displaystyle a_{1}\sim b_{1}}$ ${\displaystyle \lor }$ ${\displaystyle a_{2}\sim b_{2}}$	${\displaystyle \sim _{1}}$ ${\displaystyle \lor }$ ${\displaystyle \sim _{2}}$	${\displaystyle v_{1}^{2}~e_{2}~+~e_{1}~v_{2}^{2}~-~2~e_{1}~e_{2}}$
Modular product	${\displaystyle a_{1}\sim b_{1}~\land ~a_{2}\sim b_{2}}$ ${\displaystyle \lor }$ ${\displaystyle a_{1}\not \simeq b_{1}~\land ~a_{2}\not \simeq b_{2}}$	${\displaystyle \sim _{1}~\sim _{2}}$ ${\displaystyle \lor }$ ${\displaystyle \not \simeq _{1}~\not \simeq _{2}}$
Rooted product	see article		${\displaystyle v_{1}~e_{2}~+~e_{1}}$
Zig-zag product	see article		see article	see article
Replacement product
Homomorphic product[1][3] ${\displaystyle G_{1}\ltimes G_{2}}$	${\displaystyle a_{1}=b_{1}}$ ${\displaystyle \lor }$ ${\displaystyle a_{1}\sim b_{1}~\land ~a_{2}\not \sim b_{2}}$	${\displaystyle =_{1}}$ ${\displaystyle \lor }$ ${\displaystyle \sim _{1}~\not \sim _{2}}$	${\displaystyle v_{1}v_{2}(v_{2}-1)/2+e_{1}(v_{2}^{2}-2e_{2})}$

In general, a graph product is determined by any condition for ${\displaystyle (a_{1},a_{2})\sim (b_{1},b_{2})}$ that can be expressed in terms of ${\displaystyle a_{n}=b_{n}}$ and ${\displaystyle a_{n}\sim b_{n}}$.

Let ${\displaystyle K_{2}}$ be the complete graph on two vertices (i.e. a single edge). The product graphs ${\displaystyle K_{2}\square K_{2}}$, ${\displaystyle K_{2}\times K_{2}}$, and ${\displaystyle K_{2}\boxtimes K_{2}}$ look exactly like the graph representing the operator. For example, ${\displaystyle K_{2}\square K_{2}}$ is a four cycle (a square) and ${\displaystyle K_{2}\boxtimes K_{2}}$ is the complete graph on four vertices.

The ${\displaystyle G_{1}[G_{2}]}$ notation for lexicographic product serves as a reminder that this product is not commutative. The resulting graph looks like substituting a copy of ${\displaystyle G_{2}}$ for every vertex of ${\displaystyle G_{1}}$.

• Graph operations