Great snub dodecicosidodecahedron
| Great snub dodecicosidodecahedron | |
|---|---|
 | |
| Type | Uniform star polyhedron |
| Elements | F = 104, E = 180 V = 60 (χ = −16) |
| Faces by sides | (20+60){3}+(12+12){5/2} |
| Coxeter diagram |  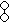 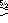  |
| Wythoff symbol | | 5/3 5/2 3 |
| Symmetry group | I, [5,3]+, 532 |
| Index references | U64, C80, W115 |
| Dual polyhedron | Great hexagonal hexecontahedron |
| Vertex figure |  3.3.3.5/2.3.5/3 |
| Bowers acronym | Gisdid |

In geometry, the great snub dodecicosidodecahedron (or great snub dodekicosidodecahedron) is a nonconvex uniform polyhedron, indexed as U64. It has 104 faces (80 triangles and 24 pentagrams), 180 edges, and 60 vertices.[1] It has Coxeter diagram 
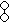
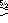
 . It has the unusual feature that its 24 pentagram faces occur in 12 coplanar pairs.
. It has the unusual feature that its 24 pentagram faces occur in 12 coplanar pairs.
Cartesian coordinates
Let the point be given by
- ,
where is the golden ratio. Let the matrix be given by
- .
is the rotation around the axis by an angle of , counterclockwise. Let the linear transformations be the transformations which send a point to the even permutations of with an even number of minus signs. The transformations constitute the group of rotational symmetries of a regular tetrahedron. The transformations , constitute the group of rotational symmetries of a regular icosahedron. Then the 60 points are the vertices of a great snub dodecicosidodecahedron. The edge length equals , the circumradius equals , and the midradius equals .
For a great snub dodecicosidodecahedron whose edge length is 1, the circumradius is
- .
Its midradius is
- .
Related polyhedra
It shares its vertices and edges, as well as 20 of its triangular faces and all its pentagrammic faces, with the great dirhombicosidodecahedron, (although the latter has 60 edges not contained in the great snub dodecicosidodecahedron). It shares its other 60 triangular faces (and its pentagrammic faces again) with the great disnub dirhombidodecahedron.
The edges and triangular faces also occur in the compound of twenty octahedra. In addition, 20 of the triangular faces occur in one enantiomer of the compound of twenty tetrahemihexahedra, and the other 60 triangular faces occur in the other enantiomer.
 Convex hull |  Great snub dodecicosidodecahedron |  Great dirhombicosidodecahedron |
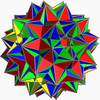 Great disnub dirhombidodecahedron |  Compound of twenty octahedra |  Compound of twenty tetrahemihexahedra |
Gallery
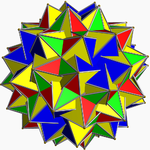 Traditional filling |  Modulo-2 filling |
See also
References
- ^ Maeder, Roman. "64: great snub dodecicosidodecahedron". MathConsult.
External links
- Weisstein, Eric W. "Great snub dodecicosidodecahedron". MathWorld.
- v
- t
- e































