Équations de compétition de Lotka-Volterra

Ne doit pas être confondu avec Équations de prédation de Lotka-Volterra.

Les équations de compétition de Lotka-Volterra sont un modèle phénoménologique simple de dynamique des populations en compétition. Leur expression est similaire à celle des équations de prédation de Lotka-Volterra pour la prédation.

Soient deux populations en compétition ${\displaystyle N_{1}}$ et ${\displaystyle N_{2}}$, suivant une dynamique logistique avec un taux de croissance ${\displaystyle r_{1}}$ (respectivement ${\displaystyle r_{2}}$) et une capacité biotique ${\displaystyle K_{1}}$ (respectivement ${\displaystyle K_{2}}$). Les équations de compétition de Lotka-Volterra ajoutent un terme modélisant l'interaction entre les deux espèces :

${\displaystyle {\begin{cases}{dN_{1} \over dt}=r_{1}N_{1}\left(1-\left({N_{1}+\alpha _{12}N_{2} \over K_{1}}\right)\right)\\{dN_{2} \over dt}=r_{2}N_{2}\left(1-\left({N_{2}+\alpha _{21}N_{1} \over K_{2}}\right)\right)\end{cases}}}$

Ici, ${\displaystyle \alpha _{12}}$ représente l'effet de l'espèce ${\displaystyle 2}$ sur la population de l'espèce ${\displaystyle 1}$, et réciproquement ${\displaystyle \alpha _{21}}$ représente l'effet de l'espèce ${\displaystyle 1}$ sur l'espèce ${\displaystyle 2}$. Les valeurs ${\displaystyle \alpha _{12}}$ et ${\displaystyle \alpha _{21}}$ ne sont pas nécessairement égales, de plus chaque espèce peut avoir un taux de croissance et une capacité biotique distincte.

Dans le cas du modèle de compétition stricte, les interactions sont délétères, ainsi les valeurs de ${\displaystyle \alpha }$ sont toutes positives. Si ${\displaystyle \alpha _{12}}$ et ${\displaystyle \alpha _{21}}$ n'ont pas le même signe, une des deux populations croit aux dépens de l'autre (ce qui peut s'interpréter comme de la prédation ou du parasitisme), si les deux termes sont négatifs, les deux populations ont un effet positif sur l'autre (ce qui peut s'interpréter comme du mutualisme, mais est rarement utilisé en pratique car cela peut permettre aux populations de croître indéfiniment). Une classification complète des dynamiques de ce système est disponible^[1].

Ce modèle peut être généralisé à un nombre quelconque d'espèces en compétition :

${\displaystyle {\frac {dN_{i}}{dt}}=r_{i}N_{i}\left(1-{\frac {\sum _{j=1}^{R}\alpha _{ij}N_{j}}{K_{i}}}\right)}$

où R est le nombre d'espèces en compétition (ou richesse spécifique). Dans ce cas il est pratique de représenter les termes de taux de croissance ${\displaystyle r_{i}}$ sous la forme d'un vecteur et les termes d'interactions ${\displaystyle \alpha _{ij}}$ sous la forme d'une matrice (appelée matrice d'interaction). On remarque l'apparition de terme de compétition intra-spécifique ${\displaystyle \alpha _{ii}}$ dont la valeur est généralement fixée à 1 par souci de cohérence avec le modèle de croissance logistique.

Le comportement asymptotique du modèle à deux espèces peut être facilement exploré en faisant une analyse des isoclines^[2] : une analyse graphique de la position des isoclines-zéro (courbes le long desquelles la croissance d'une espèce est nulle) dans l'espace des phases qui est ici le plan ${\displaystyle (N_{1},N_{2})}$.

Chaque espèce ${\displaystyle i}$ a deux isoclines, solutions de l'équation ${\displaystyle {\frac {dN_{i}}{dt}}=0}$ :

• l'axe ${\displaystyle N_{i}=0}$ (appelée aussi isocline triviale) et
• ${\displaystyle N_{i}=K_{i}-\alpha _{ij}N_{j}}$ (appelée aussi isocline non triviale).

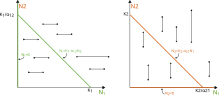
Le signe du taux de croissance effectif de l'espèce ${\displaystyle i}$ change de part et d'autre de l'isocline (positif en dessous, négatif au-dessus) ainsi la population d'une espèce non éteinte tend vers son isocline non triviale^[3]. On remarque tout de suite que si l'une des deux espèces est éteinte (${\displaystyle N_{i}=0}$) on se retrouve exactement dans le cas du modèle de croissance logistique. C'est aussi le cas si l'autre espèce à un niveau de population fixe (${\displaystyle N_{j}}$ constante) mais la capacité biotique est alors ${\displaystyle K^{*}=K_{i}-\alpha _{ij}N_{j}}$.

Pour des conditions initiales où les deux espèces sont présentes, en fonction de la position relative des deux isoclines non triviales, on observe quatre types de comportements:

1. exclusion compétitive de l'espèce ${\displaystyle 2}$ par l'espèce ${\displaystyle 1}$,
2. exclusion compétitive de l'espèce ${\displaystyle 1}$ par l'espèce ${\displaystyle 2}$,
3. coexistence stable des deux espèces,
4. exclusion compétitive d'une des deux espèces en fonction des conditions initiales.

Les équilibres du système sont les points où les deux dérivées s'annulent simultanément (il s'agit des points d'intersection entre les isoclines des deux espèces). Il y en a au moins trois : ${\displaystyle (0,0)}$ correspondant à l'extinction des deux espèces (intersection entre les isoclines triviales) ainsi que ${\displaystyle (K_{1},0)}$ et ${\displaystyle (0,K_{2})}$ correspondant à l'exclusion compétitive de l'une ou l'autre espèce. Il y en a un quatrième si les deux isoclines non triviales se croisent pour des valeurs positives de ${\displaystyle (N_{1},N_{2})}$ (dans les cas 3 ou 4).

La stabilité des équilibres peut être étudiée par le biais du signe des valeurs propres de la matrice jacobienne du système en ces points. Cela permet de formaliser les conditions de la coexistence stable des deux espèces et forme un des fondements de la théorie de la coexistence^[4].

Pour plus de simplicité on se place dans le cas où ${\displaystyle r_{1}>0}$, ${\displaystyle r_{2}>0}$ et ${\displaystyle K_{1}=K_{2}=1}$.

• ${\displaystyle (0,0)}$ a pour valeur propres associées ${\displaystyle (r_{1},r_{2})}$. Cet équilibre est donc toujours un nœud instable.
• ${\displaystyle (0,K_{1})}$ a pour valeurs propres associées ${\displaystyle (-r_{1},r_{2}(1-\alpha _{12}))}$. Cet équilibre est donc un nœud stable si ${\displaystyle \alpha _{12}>1}$.
• ${\displaystyle (K_{2},0)}$ a pour valeurs propres associées ${\displaystyle (r_{1}(1-\alpha _{21}),-r_{2})}$. Cet équilibre est donc un nœud stable si ${\displaystyle \alpha _{21}>1}$.

La coexistence stable des deux espèces n'est possible que si les deux équilibres d'exclusion compétitive sont simultanément instables, c'est-à-dire si ${\displaystyle \alpha _{12}<1}$ et ${\displaystyle \alpha _{21}<1}$. L'interprétation écologique de cette condition est la nécessité que la compétition interspécifique (dont l'intensité est représentée par les paramètres ${\displaystyle \alpha _{21}}$ et ${\displaystyle \alpha _{12}}$) soit plus faible que la compétition intraspécifique (dont l'intensité vaut ici 1, mais que l'on peut^[5] paramétrer par ${\displaystyle \alpha _{11}=K_{2}/K_{1}}$ et ${\displaystyle \alpha _{22}=K_{1}/K_{2}}$). L'intensité de la compétition interspécifique dépend des niches écologique respectives des deux espèces^[4].

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

Le modèle de compétition de Lotka-Volterra est phénoménologique^[6],[5] dans le sens où il décrit un phénomène sans préciser le mécanisme qui le cause. Ainsi, il a l'avantage de pouvoir être utilisé comme approximation pour de nombreux systèmes plus complexes, mais son pouvoir prédictif est assez faible. Même s'il n'est pas conçu pour un mécanisme particulier, il est cependant possible de proposer plusieurs interprétations mécanistiques.

• Compétition directe : les individus ont un effet direct et négatif les uns sur les autres. On peut considérer les individus comme se déplaçant de façon aléatoire sur une surface, les équations de Lotka-Volterra peuvent ainsi être vues comme décrivant la cinétique de ce système. Dans ce cas ${\displaystyle \alpha _{ij}}$ est la probabilité que lors d'une rencontre en entre un individu des espèces ${\displaystyle i}$ et ${\displaystyle j}$, l'individu de l'espèce ${\displaystyle j}$ consomme l'individu de l'espèce ${\displaystyle i}$.
• Compétition indirecte pour une ressource^[7] : il est possible d'obtenir la même dynamique en supposant que les croissances des différentes espèces dépendent d'une ou plusieurs ressources pour lesquelles elles sont en compétition. Dans ce cas les paramètres utilisés ici (${\displaystyle \alpha ,r,K}$) dépendent d'un certain nombre d'autres paramètres décrivant la dynamique de la population en fonction de la quantité de ressources (taux de conversion, probabilité de rencontre...).

Pierre Auger, Christophe Lett et Jean-Christophe Poggiale, Modélisation mathématique en écologie, Dunod, 2010

• Portail de l’écologie
• Portail de l'analyse