Aberration (optique)

Cet article concernant la physique doit être recyclé ().
Motif : Page en cours de recyclage.
Améliorez-le, discutez des points à améliorer ou précisez les sections à recycler en utilisant {{section à recycler}}.
Pour les articles homonymes, voir Aberration.

Ne doit pas être confondu avec Aberration de la lumière.

Une aberration est un défaut du système optique qui se répercute sur la qualité de l'image (flou, irisation ou déformation). Les aberrations sont définies par rapport à l'optique paraxiale[1] et matérialisent le fait que certains rayons ne convergent pas vers l'image prédite par l'optique géométrique. Ainsi, la théorie des aberrations s'inscrit dans le cadre de l'optique géométrique et ne prend pas en compte les aspects ondulatoire ou corpusculaire de la lumière.
Il est possible de classer les aberrations en deux groupes. D'une part, les aberrations chromatiques, dépendantes de la longueur d'onde, qui sont responsables d'erreurs d'ordre colorimétrique dans les images. D'autre part, les aberrations géométriques, dépendantes de paramètres géométriques (position de la pupille, ouverture numérique et angle de champ notamment) ont un impact sur le pouvoir de résolution du système.
La conception optique permet de concevoir des systèmes peu aberrants en combinant des optiques dont les aberrations se compensent.
Historique
La notion d'aberration est née avec les premiers instruments d'optique imageante : le verre correcteur en 1285[2] et surtout la lunette astronomique et le microscope mis au point par Antoni van Leeuwenhoek avec des procédés de fabrication de lentilles optiques révolutionnaires pour l'époque[3]. Les premiers instruments font immédiatement apparaître des aberrations, notamment chromatique dans le cas des lunettes astronomiques.
Pourtant il faudra attendre le XIXe siècle pour qu'une théorie des aberrations apparaisse. La notion de stigmatisme est théorisée par Gauss en 1840[4] et Ernst Abbe développe au cours de la seconde moitié du XIXe siècle la notion d'aberration sphérique et chromatique. La mise en place d'un formalisme mathématique (polynômes de Zernike) autour des aberrations ne date que du début du XXe siècle.
Description du phénomène d’aberration
Origines possibles des aberrations
Les défauts observés dans une image lors de l'utilisation de systèmes optiques peuvent avoir plusieurs origines. Il convient donc de distinguer les défauts de fabrication liés aux éléments optiques (ces défauts font l'objet de spécifications particulières pour la qualité des optiques[5],[6]) :
- Défauts du matériaux des optiques: bulles, inclusions ou inhomogénéité de l'indice optique .
- Défauts de fabrication : planéité, rayons de courbures, rugosité de surface .
- Défauts dus à l'usure : rayures, revêtement optique endommagé .
- Défauts de conception : Aberrations présentes dès la phase de design .
Approche géométrique
Le domaine de l’optique géométrique traite des systèmes optiques au travers des lois de Snell-Descartes (réfraction, réflexion) et du principe de Fermat selon lequel les rayons lumineux traversent un milieu en empruntant un chemin optique extrémal. Ce modèle géométrique permet de prédire la trajectoire des rayons lumineux au travers du système dans le cadre de l'approximation paraxiale.
Dans le modèle géométrique, les aberrations traduisent l'écart de trajectoire entre les rayons réels et les rayons théoriques. Les rayons théoriques étant pour la plupart construits à partir de lois faisant appel à des fonctions simples (sinus, cosinus, tangente), il est possible de linéariser l'écart des rayons réels par un développement limité et d'écrire les aberrations du système sous la forme d'un polynôme.
-
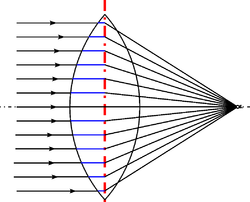 Lentille parfaite sur l'axe : Tous les rayons focalisent vers le même point. Cette optique est dénuée d'aberration sur l'axe.
Lentille parfaite sur l'axe : Tous les rayons focalisent vers le même point. Cette optique est dénuée d'aberration sur l'axe. -
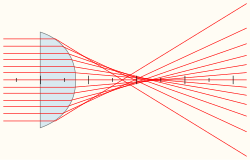 Lentille aberrante sur l'axe : Les rayons paraxiaux focalisent en un point (foyer paraxial) tandis que les rayons marginaux focalisent en un autre point (foyer marginal). L'image n'est plus un point mais une tache, le pouvoir de résolution est dégradé.
Lentille aberrante sur l'axe : Les rayons paraxiaux focalisent en un point (foyer paraxial) tandis que les rayons marginaux focalisent en un autre point (foyer marginal). L'image n'est plus un point mais une tache, le pouvoir de résolution est dégradé.
Approche ondulatoire
En optique ondulatoire, la lumière est modélisée non plus par un rayon géométrique mais par une onde électromagnétique.
Cela conduit à plusieurs conséquences importantes. D'abord, l'image d'un point, même au travers d'un système parfait, n'est plus un point mais une tache. Le diamètre de cette tache d'Airy est donné par :
Avec Φ le diamètre de la tache d'Airy, λ la longueur d'onde de la lumière et ON l'ouverture numérique du système.
On retrouve les résultats de l'optique géométrique lorsque λ tend vers zéro ie lorsque la longueur d'onde devient négligeable devant les dimensions des objets que la lumière va rencontrer. De plus, on s'attend à voir émerger des problèmes de taille de tache lorsqu'on travaille en lumière polychromatique : le diamètre de la tache d'Airy dépend de la longueur d'onde, donc le bord d'une tache issu d'une lumière polychromatique présente un dégradé de couleur.
La comparaison entre la tache d'Airy attendue et la tache image réelle constitue en soi un premier critère permettant de savoir si le système étudié présente des aberrations.
D'autre part, l'approche ondulatoire conduit à décrire la propagation de la lumière en termes de front d'onde. La comparaison du front d'onde réel avec le front d'onde théorique permet de déduire un écart normal. Cet écart normal est ensuite développé sous forme polynomiale. La forme du polynôme permet d'identifier et de quantifier les aberrations présentes dans le système.
- Tache polychromatique (Image en fausses couleurs)
-
 Modification du front d'onde par une lentille convergente.
Modification du front d'onde par une lentille convergente. -
 Front d'onde réel issu d'une mesure interférométrique. Ce front d'onde n'étant pas sphérique, on déduit que l'optique étudiée présente des aberrations.
Front d'onde réel issu d'une mesure interférométrique. Ce front d'onde n'étant pas sphérique, on déduit que l'optique étudiée présente des aberrations.
Lien entre déformation du front d'onde et tache image
Les relations de Nijboer (en) permettent de relier la dimension de la tache image à l'écart du front d'onde réel au front d'onde idéal[7].
Aberrations chromatiques
L'indice d'un verre dépend de la longueur d'onde. Cette dépendance peut être approchée en première approximation par la loi de Cauchy [8]. Cette dépendance explique la dispersion du milieu. On parle alors de la constringence (ou nombre d'Abbe) du milieu (en général du verre optique) qui décrit comment évolue l'indice optique avec la longueur d'onde. Un verre avec un faible nombre d'Abbe a un indice optique variant beaucoup avec la longueur d'onde, et a introduit alors beaucoup d'aberration chromatique.

Il en résulte donc que la focalisation pour les différentes longueurs d'onde d'une source polychromatique ne se fait pas dans le même plan, ce qui peut être observé sous la forme d'irisations.
Les aberrations chromatiques peuvent être regroupées en deux catégories :
- le chromatisme axial qui se traduit par des plans de mise au point différents pour les images de chaque longueur d'onde ;
- le chromatisme latéral qui se traduit par des images de taille différente pour chaque longueur d'onde.
L'aberration chromatique ne concerne que les systèmes comprenant des lentilles. Ainsi, un système n'utilisant que des miroirs n'aura aucune aberration chromatique.
La correction de l'aberration chromatique se fait de différente manière :
- Utiliser des miroirs à la place des lentilles. Les miroirs introduisent cependant d'autres aberrations.
- Utiliser des verres optiques ayant de grand nombres d'Abbe.
- Utiliser des combinaisons de différentes lentilles convergentes et divergentes ayant des nombres d'Abbe différents pour compenser l'aberration chromatique. (Principe du doublet achromatique ou de l'objectif apochromatique).
 |  |
|---|
Aberrations géométriques
Principe d'une aberration géométrique, approche géométrique
Une aberration géométrique est un écart entre un rayon paraxial, défini dans l'approximation de Gauss, et le rayon réel correspondant. Elle peut aussi être caractérisée par un écart entre la surface d'onde paraxiale et la surface d'onde réelle.)

Pour un système parfait, tous les rayons partant du point B situé dans le plan objet xy à une distance h de l'axe optique doivent converger en un point B' situé à une distance h' de l'axe optique dans le plan image x'y'. Or, les phénomènes d'aberrations sont tels qu'un rayon va arriver en un point B" ; à une certaine distance Δh' de B'.
Les aberrations géométriques dépendent de[9] :
- La qualité du design opto-mécanique (aberrations de décentrement, de piston ou de tilt).
- La position du rayon sur l'objet (h).
- La position du rayon dans le plan image (h').
- La position du rayon dans le plan pupille (ρ)
- La géométrie du système (symétrie par rapport à la pupille, symétrie de révolution ou non, etc.).
Aberrations du 3ème ordre
Approche géométrique
En reprenant les notations géométriques du schéma ci-dessus, on a[10],[11], pour un système à symétrie de révolution autour de l'axe optique :
| Nom | Dépendance | Caractéristique | Correction |
|---|---|---|---|
| Aberration sphérique | ∝ ρ3 | Sur l'axe et hors d'axe. Flou | Optique non sphérique, faible ouverture |
| Aberration de coma | ∝ ρ2h' | Hors d'axe. Flou et tache en forme d'aigrette | Optique non sphérique |
| Astigmatisme et courbure de champ | ∝ ρh'2 | Hors d'axe. Astigmatisme : Deux plans de focalisation distincts Courbure de champ : Plan focal courbe | Courbure du plan image et/ou optiques complexes |
| Distorsion | ∝ h'3 | Hors d'axe. Déformation. | Symétrie de construction, traitement numérique. |

Cette notation de dépendance sert à avoir une approche qualitative des influences des différents paramètres du système sur les aberrations. Par exemple, on peut voir qu'en fermant le diaphragme d'un système (et ainsi limitant ρ à de petites valeurs), on réduit fortement l'aberration sphérique (proportionnelle à ρ3) mais on ne modifie pas la distorsion (qui ne dépend pas de ρ).
Cas de la distorsion
La distorsion n'est pas une aberration comme les autres. En effet, cette aberration n’entraîne pas de destruction d'information, il n'y a pas de flou. Toute l'information peut théoriquement être retrouvé par déformation de l'image[9].
Aberrations d'ordre supérieur
Il est possible de poursuivre la décomposition à des ordre supérieur à 3. Celles-ci portent les mêmes noms que les aberrations d'ordre 3 suivi de l'ordre de l'aberration (par exemple, aberration sphérique d'ordre 5).
La validité de la décomposition en 3eme et 5eme ordre est pour les systèmes ayant un nombre d'ouverture supérieure à 2 et une champ inférieur à 25°. Au delà, il faudra considérer les ordres 7, puis 9...
Développement sur la base de Seidel
C’est en 1857 que Ludwig von Seidel développe une méthode permettant de séparer et analyser les aberrations optiques[12].
Deux méthodes existent pour trouver les termes exacts des aberrations de Seidel : par le calcul de la loi de Descartes pour chaque élément de la combinaison optique, hors de l'approximation de Gauss (donc pour un développement limité à un ordre supérieur à 1), soit par la méthode développée par Buchdahl[13] qui permet de connaître les termes exacts de la série de Seidel pour les aberrations d'ordre 3 et supérieur
Tous les polynômes sont ici donnés avec un angle de 0⁰[14],[9].
| Aberration | Coefficient | Polynôme de Seidel |
|---|---|---|
| Defocus | ||
| Tilt | ||
| Aberration sphérique | ||
| Coma (optique) | ||
| Astigmatisme | ||
| Courbure de champ | ||
| Distorsion | ||
| Aberration sphérique d'ordre 5 | ||
| Coma linéaire d'ordre 5 | ||
| Astigmatisme d'ordre 5 | ||
| Courbure de champ d'ordre 5 | ||
| Distorsion d'ordre 5 | ||
| Aberration sphérique sagittale oblique | ||
| Aberration sphérique tangentielle oblique | ||
| Coma elliptique cubique | ||
| Comma elliptique linéaire |
La caractéristique principale de cette description des aberrations est qu’elle permet de prendre en compte les caractéristiques du système optique, sa symétrie de révolution, la conique des surfaces, etc. Les séries de Seidel présentent donc un avantage particulier pour la conception optique, domaine de l’optique consistant à concevoir et améliorer des systèmes optiques (viseurs, objectifs, systèmes à miroir, télescopes, etc.) car elles sont reliées de manière évidentes aux aberrations du 3e ordre.
Développement en polynômes de zernike

C’est en 1936 que Zernike améliore la description analytique des aberrations en créant une famille de polynômes nommés polynômes de Zernike. Ceux-ci sont orthogonaux dans le cercle unité (mais pas sur une portion de celui-ci) et permettent de décrire efficacement les aberrations d’ordre supérieur en prenant en compte le piston ou le tilt. Là où la série de Seidel permettait de prendre en compte la symétrie de révolution du système, les polynômes de Zernike sont plutôt une description du front d'onde sans relation directe avec le système optique. Chaque monôme décrit alors une aberration spécifique sur la surface du cercle unité.
Principe
Il est possible de relier les polynômes de Zernike aux polynômes de Seidel, cependant ceci n'est pertinent que dans un système où l'on n'étudie que les aberrations du 3e ordre. Au-delà, les contributions de certains des monômes de Zernike pour le 5e ordre s'ajoutent à celles du 3e ordre.
Développement des aberrations en Zernike
Il existe de nombreuses notations et conventions différentes pour le formalisme de Zernike. Ici, sont données les polynômes orthonormés du cercle de Zernike et aberrations compensées[15].
Chaque terme contient la quantité appropriée de termes d'ordre inférieur afin de minimiser l'erreur moyenne de front d'onde de ce terme. Les polynômes de Zernike représentent donc des aberrations classiques compensées[15],[14].
| Aberration | n | m | Notation | Polynôme de Zernike | Représentation des polynômes |
|---|---|---|---|---|---|
| Piston | 0 | 0 | 1 |  | |
| Tilt | 1 | 1 | |||
| Defocus | 2 | 0 | |||
| Astigmatisme | 2 | 2 | |||
| Coma (optique) | 3 | 1 | |||
| 3 | 3 | ||||
| Aberration sphérique | 4 | 0 | |||
| Astigmatisme secondaire | 4 | 2 | |||
| 4 | 4 | ||||
| Coma secondaire | 5 | 1 | |||
| 5 | 3 | ||||
| 5 | 5 | ||||
| Aberration sphérique secondaire | 6 | 0 | |||
| ... et ordres superieurs ... |
Avantage
Si les polynômes de Zernike sont de plus en plus employés dans les logiciels d’optimisation optique, leur prédominance dans le domaine de l’analyse de front d’onde et de l’optique adaptative est sans conteste, du fait de l’approche plus ondulatoire que la série de Seidel. Cette base de polynômes est orthogonale pour un système ayant une pupille circulaire. Cela explique leur usage fréquent dans les logiciels de conception optique qui nécessite la décomposition sur une base d'aberrations.
Limites
Il existe des systèmes optiques avec des pupilles non circulaires, tels que les télescopes avec des pupilles annulaires et hexagonales, ainsi que certains lasers avec des pupilles carrées. Dans ces cas précis, il existe des polynômes orthonormaux spécifiques.
Critères de quantification des aberrations optiques
Rapport de Strehl

Le rapport de Strehl nommé d’après le physicien Karl Strehl est une quantité exploitant le principe de front d’onde idéal et de front d’onde aberrant. On définit le rapport de Strehl comme le rapport entre la fonction d'étalement du point (ou PSF, pour Point Spread Function) au plan de meilleure mise au point pour un système limité par la diffraction et la PSF réelle entachée d’aberration. La formule est alors : où σ est l’écart quadratique entre le front d’onde parfait et le front d’onde aberrant, l’unité étant la même que celle choisie pour la longueur d’onde .
Si le rapport de Strehl est un outil généralement utile et efficace pour juger de la qualité d’une optique, il demeure limité et n’est applicable qu’à un système dont la PSF réelle n’est pas trop différente de la PSF avec aberration. Un front d’onde trop perturbé peut produire un rapport de 0,9 tout en étant très mauvais.
Critère de Maréchal
En 1947, André Maréchal développe l’idée d’un critère permettant d’évaluer la qualité d’un système optique et discute pour la première fois dans sa thèse[16] d’un critère de qualité optique, plus tard appelé critère de Maréchal. Il va alors plus loin que le critère de Rayleigh qui jusque-là se bornait à donner un critère de résolution de et énonce que l’écart RMS entre front d’onde idéal et front d’onde réel doit être inférieur à ce qui ramené au rapport de Strehl, implique d’avoir un rapport de Strehl approché d’environ 0.82.
FTM
La FTM (fonction de transfert de modulation) correspond à l'évolution du contraste en fonction de la fréquence spatiale. Elle quantifie la capacité d'un système optique à reproduire correctement les différentes fréquences spatiales du sujet.
Sur une image, les faibles fréquences spatiales correspondent aux grandes zones claires et sombres, alors que les hautes fréquences spatiales représentent les détails fins et les changements brusques de luminosité, par exemple au bord d'un objet. En photographie, un système transmettant bien les hautes fréquences spatiales aurait du piqué.
L'ouverture numérique pour une longueur d'onde donnée limite la fréquence spatiale de coupure.
Mathématiquement il s'agit de la valeur normée de la fonction de transfert, pour un éclairage incohérent[17]. Dans le cas idéal (limite de diffraction), la FTM correspond à l'autocorrélation de la pupille du système, soit :En pratique, pour calculer la FTM d'un système imageant, une mire de résolution, (par exemple une mire USAF 1951) est utilisée. Ce type de mire contient des éléments de toutes taille (et donc de toutes fréquences spatiales). Pour chacun de ces motifs, le contraste est calculé et on obtient donc la FTM.

L'image ci-dessus montre que le système peu aberrant a une meilleur FTM que le système avec des aberration, ainsi le contraste est meilleur pour les grandes fréquences spatiales (centre de c et f) . Cela est confirmé par la PSF du système qui est plus petite en b qu'en e.
Détermination expérimentale des aberrations
Méthode du point lumineux

Cette méthode est la plus ancienne et la moins onéreuse à mettre en place. En pratique, la méthode repose sur le fait que l'observation de la tache image d'une source de petite dimension se rapproche de sa réponse impulsionnelle. L'observation de la forme de cette réponse impulsionnelle et la position de mise au point permet sur l'axe seul de connaître :
- la présence d'aberration sphérique ;
- la présence d'astigmatisme ;
- la présence de chromatisme.
Un monochromateur peut permettre de quantifier le chromatisme par mesure de la position du meilleur foyer en fonction de la longueur d'onde.
Dans le champ (nécessite un dispositif de rotation de la source lumineuse autour de l'optique d'étude), on peut connaître en plus :
- la présence de coma ;
- la valeur de la courbure de champ ;
- la valeur des courbures sagittales et tangentielles.
Cette méthode permet également dans le cas d'optiques à diaphragme de déterminer à partir de quelle ouverture l'optique est limitée par la diffraction[18].
Analyse de front d'onde

Les analyseurs de front d'onde permettent de mesurer une partie des défauts des optiques avec une grande précision.
On distingue deux types d'analyseur de front d'onde : les analyseurs interférométriques (Fizeau, Zygo, etc.) et les analyseurs à micro-lentilles (Shack-Hartmann, Phasics, etc.). Les premiers donnent le défaut du front d'onde par rapport à un front d'onde de référence. Les derniers donnent une carte topologique de la déformation (valeur absolue du défaut de front d'onde).
Cependant de tels dispositifs ne quantifient pas le chromatisme ni la distorsion puisqu'ils travaillent en lumière monochromatique, et que la distorsion est une déformation qui n'impacte pas le front d'onde
Correction des aberrations
Notes et références
Notes
- ↑ Robert Guenther, Modern Optics, Cambridge, John Wiley & Sons Inc., (ISBN 0-471-60538-7), p. 130.
- ↑ Optique MPSI-PCSI-PTSI sur Google Livres
- ↑ Udo Wiesmann, In Su Choi et Eva-Maria Dombrowski (2006). Fundamentals of Biological Wastewater Treatment, Wiley-VCH Verlag GmnH : p. 8-9. (ISBN 3527312196)
- ↑ Dioptrische Untersuchungen sur Google Livres
- ↑ D'après Norme MIL-PRF-13830 Section 3.5 et MIL-O-1383, 1954, Avec masque de référence C7641866 révision L, de 1980
- ↑ D'après Norme ISO 10110-3:199, 1996 et Norme ISO 10110-5:2007, 2007
- ↑ The Extended Nijboer-Zernike Diffraction Theory and Its Applications sur Google Livres
- ↑ Bernard Balland, Optique géométrique : Imagerie et instruments, p. 58
- ↑ a b et c Julie Bentley et Craig Olson, Field Guide to Lens Design, SPIE, (ISBN 978-0-8194-9165-7, DOI 10.1117/3.934997, lire en ligne)
- ↑ John E. Greivenkamp, Field Guide to Geometrical Optics, SPIE, (ISBN 978-0-8194-7816-0, DOI 10.1117/3.547461, lire en ligne)
- ↑ « Aberrations géométriques », sur ressources.univ-lemans.fr (consulté le )
- ↑ (1856), 289–332; “Über den Einfluss der Theorie der Fehler, mit welchen die durch optische Instrumente gesehenen Bilder behaftet sind, und über die mathematischen Bedingungen ihrer Authebung,” in Abhandlungen der naturwissenschaftlich-technischen Commission der Bayerischen Akademie der Wissenschaften
- ↑ An Introduction to Hamiltonian Optics, H.A. Buchdahl, Dover Classics of Science & Mathematics, 17 août 1997
- ↑ a et b Handbook of optics, McGraw-Hill, (ISBN 978-0-07-149889-0, 978-0-07-163598-1 et 978-0-07-163604-9, OCLC 318409251, lire en ligne)
- ↑ a et b (en) Optical Shop Testing, Wiley, (ISBN 978-0-471-48404-2 et 978-0-470-13597-6, DOI 10.1002/9780470135976, lire en ligne)
- ↑ « l’étude des influences conjuguées des aberrations et de la diffraction sur l’image d’un point », soutenue le 13 juin 1947
- ↑ De l'Optique électromagnétique à l'Interférométrie: Concepts et illustrations sur Google Livres
- ↑ http://paristech.institutoptique.fr/site.php?id=762&fileid=9696
Voir aussi
- Aberration géométrique
- Aberration chromatique
- Conception optique
- Distorsion (optique)
- Aberrations en optique des particules chargées
Liens externes
v · m | |
|---|---|
| Optique géométrique |
|
| Conception optique | |
| Objectif photographique | |
| Performances | |
| Défauts d'objectifs |
|
| Monture d'objectif | |
| Modèles remarquables | |
 Portail de l’astronomie
Portail de l’astronomie  Portail de l’optique
Portail de l’optique  Portail de la photographie
Portail de la photographie
















































































