Algorithme de Chan

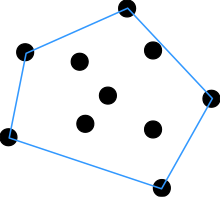
En géométrie algorithmique, l'algorithme de Chan^[1] nommé d'après son inventeur Timothy M. Chan (en), est un algorithme sensible à la sortie qui calcule l'enveloppe convexe d'un ensemble ${\displaystyle P}$ de ${\displaystyle n}$ points, en dimension 2 ou 3. La complexité temporelle est ${\displaystyle {\mathcal {O}}(n\log h)}$ où ${\displaystyle h}$ est le nombre de points dans l'enveloppe convexe. En dimension 2, l'algorithme combine un algorithme en ${\displaystyle {\mathcal {O}}(n\log n)}$ (par exemple le parcours de Graham) et la marche de Jarvis afin d'obtenir un algorithme en ${\displaystyle {\mathcal {O}}(n\log h)}$. L'algorithme de Chan est important car il est plus simple que l'algorithme de Kirkpatrick-Seidel et s'étend facilement à la dimension 3. Le paradigme utilisé dans l'algorithme s'appuie sur les travaux de Frank Nielsen^[2],[3].

Dans un premier temps, nous présentons un algorithme qui utilise la valeur de ${\displaystyle h}$ et nous appelons ce paramètre ${\displaystyle m=h}$. Cette hypothèse n'est pas réaliste et nous allons la supprimer plus tard. L'algorithme est divisé en deux phases.

L'algorithme commence par partitionner ${\displaystyle P}$ en au plus ${\displaystyle 1+n/m}$ sous-ensembles ${\displaystyle Q}$ avec au plus ${\displaystyle m}$ points dans chaque sous-ensemble. Puis, on calcule l'enveloppe convexe de chacun des sous-ensembles ${\displaystyle Q}$ en utilisant un algorithme en ${\displaystyle {\mathcal {O}}(n\log n)}$ (par exemple le parcours de Graham). Remarquons que, comme il y a ${\displaystyle {\mathcal {O}}(n/m)}$ sous-ensembles de ${\displaystyle {\mathcal {O}}(m)}$ points chacun, cette phase prend ${\displaystyle {\mathcal {O}}(n/m){\mathcal {O}}(m\log m)={\mathcal {O}}(n\log m)}$ opérations.

La seconde phase consiste à exécuter une marche de Jarvis en utilisant les enveloppes convexes précalculées dans la phase 1 pour accélérer le calcul. À chaque étape de la marche de Jarvis, on considère un point ${\displaystyle p_{i}}$ de l'enveloppe convexe et on cherche à calculer le point ${\displaystyle p_{i+1}=f(p_{i},P)}$ tel que tous les autres points de ${\displaystyle P}$ sont à droite de la ligne ${\displaystyle p_{i}p_{i+1}}$. Si l'on connait l'enveloppe convexe ${\displaystyle Q}$ de ${\displaystyle m}$ points, alors on peut calculer ${\displaystyle f(p_{i},Q)}$ en ${\displaystyle {\mathcal {O}}(\log m)}$ en utilisant la recherche dichotomique. On calcule ${\displaystyle f(p_{i},Q)}$ pour tous les ${\displaystyle {\mathcal {O}}(n/m)}$ sous-ensembles ${\displaystyle Q}$ de la phase 1 en ${\displaystyle {\mathcal {O}}(n/m\log m)}$. Puis, on détermine ${\displaystyle f(p_{i},P)}$ en utilisant la même technique que celle de la marche de Jarvis, mais en ne considérant que les points ${\displaystyle f(p_{i},Q)}$ où ${\displaystyle Q}$ est un sous-ensemble de la phase 1. Comme la marche de Jarvis répète le calcul d'un ${\displaystyle f(p_{i},P)}$ ${\displaystyle {\mathcal {O}}(h)}$ fois, la seconde phase prend ${\displaystyle {\mathcal {O}}(n\log m)}$ opérations. Si ${\displaystyle m=h}$, elle prend ${\displaystyle {\mathcal {O}}(n\log h)}$ opérations.

L'algorithme décrit précédemment utilise ${\displaystyle m=h}$. Si ${\displaystyle m<h}$, nous nous en rendons compte dans la marche de Jarvis au bout de ${\displaystyle m+1}$ étapes. Ainsi, si ${\displaystyle m<h}$, on prend ${\displaystyle {\mathcal {O}}(n\log m)}$ pour s'en rendre compte (et on ne calcule pas l'enveloppe convexe jusqu'au bout). Si ${\displaystyle m>h}$, on s'en rend compte aussi puisque l'algorithme s'arrête et calcule l'enveloppe convexe.

L'idée consiste alors à commencer l'algorithme avec une valeur petite pour ${\displaystyle m}$ (dans l'analyse qui suit on utilise 2, mais des nombres aux alentours de 5 marchent mieux en pratique), puis on augmente la valeur de ${\displaystyle m}$ jusqu'à ce que ${\displaystyle m>h}$, et dans ce cas, on obtient l'enveloppe convexe.

Si on augmente la valeur de ${\displaystyle m}$ trop lentement, on a besoin de répéter les phases 1 et 2 trop de fois et le temps de d'exécution est trop grand. A contrario, si on augmente les valeurs de ${\displaystyle m}$ trop vite, on risque d'atteindre une valeur de ${\displaystyle m}$ beaucoup trop grande par rapport à ${\displaystyle h}$, et le temps d'exécution est trop grand. À la manière de la stratégie utilisée dans l'algorithme de Chazelle and Matoušek's^[4], l'algorithme de Chan élève au carré la valeur de ${\displaystyle m}$ à chaque itération sans dépasser ${\displaystyle n}$. En d'autres termes, ${\displaystyle m}$ prend les valeurs 2, 4, 16, 256, etc. et à l'itération numéro ${\displaystyle t}$ (en commençant à 0), on a ${\displaystyle m=\min(n,2^{2^{t}})}$. Le temps d'exécution total de l'algorithme est

${\displaystyle \sum _{t=0}^{\lceil \log \log h\rceil }{\mathcal {O}}\left(n\log(2^{2^{t}})\right)={\mathcal {O}}(n)\sum _{t=0}^{\lceil \log \log h\rceil }O(2^{t})={\mathcal {O}}\left(n\cdot 2^{1+\lceil \log \log h\rceil }\right)={\mathcal {O}}(n\log h).}$

Pour généraliser l'algorithme en dimension 3, on doit utiliser un autre algorithme en ${\displaystyle {\mathcal {O}}(n\log n)}$ à la place du parcours de Graham et on doit utiliser une version 3D de la marche de Jarvis. La complexité temporelle reste en ${\displaystyle {\mathcal {O}}(n\log h)}$.

Dans l'article de Chan, il y a des suggestions qui pourraient améliorer la performance de l'algorithme en pratique :

• Quand on calcule les enveloppes convexes des sous-ensembles, on peut éliminer les points qui ne sont dans l'enveloppe convexe pour les autres itérations.

• Quand ${\displaystyle m}$ augmente, on peut calculer les nouvelles enveloppes convexes en fusionnant les enveloppes convexes précédentes au lieu de les recalculer à partir de zéro.

L'article de Chan contient d'autres problèmes que l'on peut rendre sensible à la sortie en utilisant la même technique, par exemple :

• Calculer la courbe minimum (lower enveloppe) d'un ensemble de ${\displaystyle n}$ segments. Hershberger^[5], donne un algorithme en ${\displaystyle {\mathcal {O}}(n\log {}n)}$ qui peut être amélioré en ${\displaystyle {\mathcal {O}}(n\log {}h)}$, où ${\displaystyle h}$ est le nombre de segments dans la courbe minimum.

• Calculer une enveloppe convexe en dimension supérieure. On peut maintenir la complexité en ${\displaystyle {\mathcal {O}}(n\log {}h)}$ si ${\displaystyle h}$ reste polynomial en ${\displaystyle n}$.

• Portail de la géométrie
• Portail de l'informatique théorique