Fonction thêta de Riemann-Siegel
En mathématiques, la fonction thêta de Riemann – Siegel est définie en termes de la fonction gamma :
pour t réel. Ici, l'argument est choisi de manière à obtenir une fonction continue et , c'est-à-dire de la même manière que la branche principale de la fonction log-gamma.
Son développement asymptotique est
qui n'est pas convergent, mais dont les premiers termes donnent une bonne approximation pour . Sa série de Taylor en 0 qui converge pour est
où désigne la fonction polygamma d'ordre . La fonction thêta de Riemann–Siegel est intéressante pour étudier la fonction zêta de Riemann, car elle peut faire pivoter la fonction zêta de Riemann de sorte qu'elle devienne la fonction Z à valeur totalement réelle sur la droite critique .
Analyse graphique
La fonction thêta de Riemann-Siegel est une fonction analytique réelle impaire sur les réels avec trois racines et . C'est une fonction croissante pour , et a des extrema locaux à , de valeur . Son seul point d'inflexion est en avec , qui est le minimum de sa dérivée.
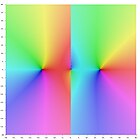
Thêta comme fonction de la variable complexe
Nous avons une expression de série infinie pour la fonction log-gamma
où γ est la constante d'Euler. En remplaçant z par et en prenant la partie imaginaire terme à terme donne la série suivante pour θ(t)
Pour les valeurs avec une partie imaginaire entre −1 et 1, la fonction arctangente est holomorphe, et on voit facilement que la série converge uniformément sur les compacts dans la région de partie imaginaire comprise entre −1/2 et 1/2, donnant à une fonction holomorphe sur ce domaine. Il s'ensuit que la fonction Z (en) est également holomorphe dans cette région, qui est la bande critique.
Nous pouvons utiliser les identités
pour obtenir l'expression de forme fermée
qui étend notre définition originale à une fonction holomorphe en t.
 |  |  |
Points de Gram
La fonction zêta de Riemann sur la ligne critique peut s'écrire où
Si est un nombre réel, alors la fonction renvoie des valeurs réelles. Par conséquent, la fonction zêta sur la ligne critique sera réelle lorsque . Les valeurs réelles positives de où cela se produit sont appelés points de Gram, d' après J. P. Gram, et peuvent aussi être décrits comme les points où est un entier. Un point de Gram est une solution de Ces solutions sont approchées par la suite :
où est la fonction W de Lambert. Voici les plus petits points de Gram positifs
| −3 | 0 | 0 |
| −2 | 3,4362182261. . . | π |
| −1 | 9,6669080561. . . | π |
| 0 | 17.8455995405. . . | 0 |
| 1 | 23,1702827012. . . | π |
| 2 | 27,6701822178. . . | 2π |
| 3 | 31,7179799547. . . | 3π |
| 4 | 35,4671842971. . . | 4π |
| 5 | 38,9992099640. . . | 5π |
| 6 | 42,3635503920. . . | 6π |
| 7 | 45,5930289815. . . | 7π |
| 8 | 48,7107766217. . . | 8π |
| 9 | 51,7338428133. . . | 9π |
| 10 | 54,6752374468. . . | 10π |
| 11 | 57,5451651795. . . | 11π |
| 12 | 60,3518119691. . . | 12π |
| 13 | 63,1018679824. . . | 13π |
| 14 | 65,8008876380. . . | 14π |
| 15 | 68,4535449175. . . | 15π |
Les points Gram sont utiles pour calculer les zéros de . À un point de Gram
et si celle-ci est positive en deux points de Gram successifs, doit avoir s'annuler dans l'intervalle.
Selon la loi de Gram, la partie réelle est généralement positive tandis que la partie imaginaire alterne avec les points de Gram, entre des valeurs positives et négatives à intervalles assez réguliers.
Le nombre de racines, , dans la bande 0 à T, est donné par
où est un terme d'erreur qui croît asymptotiquement comme .
Si obéissait à la loi de Gram, alors le nombre de racines dans la bande deviendrait simplement
Or lorsque T croit, on sait que la loi de Gram échoue pour environ 1/4 de tous les intervalles de Gram, le premier échec est à l'indice 126, avant le 127e zéro.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Riemann—Siegel theta function » (voir la liste des auteurs).
- H. M. Edwards, Riemann's Zeta Function, New York, Dover Publications, (ISBN 978-0-486-41740-0, MR 0466039)
- Gabcke, W. (1979), Neue Herleitung und explizierte Restabschätzung der Riemann-Siegel-Formel . Thèse, Université de Göttingen. Version révisée (eDiss Göttingen 2015)
- J. P. Gram, Note sur les zéros de la fonction ζ(s) de Riemann, vol. 27, , 289–304 p. (DOI 10.1007/BF02421310
 , lire en ligne)
, lire en ligne)
Liens externes
- (en) Eric W. Weisstein, « Riemann-Siegel Functions », sur MathWorld
- Wolfram Research – Riemann-Siegel Theta function
 Portail des mathématiques
Portail des mathématiques





















































