Campo di pendenza

Questa voce è orfana, ovvero priva di collegamenti in entrata da altre voci.

Inseriscine almeno uno pertinente e utile e rimuovi l'avviso. Segui i suggerimenti del progetto di riferimento.

{\displaystyle {\frac {dy}{dx}}=x^{2}-x-2} — Il campo di pendenza di ${\frac {dy}{dx}}=x^{2}-x-2$ , con le linee blu, rosse e turchesi ${\frac {x^{3}}{3}}-{\frac {x^{2}}{2}}-2x+4$ , ${\frac {x^{3}}{3}}-{\frac {x^{2}}{2}}-2x$ , E ${\frac {x^{3}}{3}}-{\frac {x^{2}}{2}}-2x-4$ , rispettivamente.

I campi di pendenza (chiamati anche campi di direzione^[1]) sono una rappresentazione grafica delle soluzioni di un'equazione differenziale del primo ordine^[2] di una funzione scalare. Le soluzioni di un campo di pendenza sono funzioni disegnate come curve solide. Un campo di pendenza mostra la pendenza di un'equazione differenziale a determinati intervalli verticali e orizzontali sul piano $x,y$ e può essere utilizzato per determinare la pendenza tangente approssimativa in un punto su una curva, dove la curva è una soluzione dell'equazione differenziale.

Definizione

Caso generale

Il campo di pendenza può essere definito per il seguente tipo di equazioni differenziali

y'=f(x,y)

che può essere interpretato geometricamente come la pendenza della tangente al grafico della soluzione dell'equazione differenziale (curva integrale) in ogni punto (x, y) in funzione delle coordinate del punto.^[3]

Può essere visto come un modo creativo per tracciare una funzione a valori reali di due variabili reali $f(x,y)$ come un'immagine planare. In particolare, per una data coppia $x,y$ , un vettore con le componenti $[1,f(x,y)]$ è disegnato al punto $x,y$ sul piano $x,y$ . A volte, il vettore $[1,f(x,y)]$ è normalizzato per rendere il grafico più chiaro alla vista dell'occhio umano. Un set di coppie $x,y$ che formano una griglia rettangolare è tipicamente utilizzata per il disegno.

Una isoclina (una serie di linee con la stessa pendenza) viene spesso utilizzata per integrare il campo di pendenza. In un'equazione della forma $y'=f(x,y)$ , l'isoclina è una linea nel piano $x,y$ ottenuta ponendo $f(x,y)$ uguale a una costante.

Caso generale di un sistema di equazioni differenziali

Dato un sistema di equazioni differenziali,

{\begin{aligned}{\frac {dx_{1}}{dt}}&=f_{1}(t,x_{1},x_{2},\ldots ,x_{n})\\{\frac {dx_{2}}{dt}}&=f_{2}(t,x_{1},x_{2},\ldots ,x_{n})\\&\;\;\vdots \\{\frac {dx_{n}}{dt}}&=f_{n}(t,x_{1},x_{2},\ldots ,x_{n})\end{aligned}}

il campo di pendenza è un vettore di segni di pendenza nello spazio di stato (in qualsiasi numero di dimensioni a seconda del numero di variabili rilevanti; ad esempio, due nel caso di una EDO lineare del primo ordine, come si vede a destra). Ogni indicatore di pendenza è centrato in un punto $(t,x_{1},x_{2},\ldots ,x_{n})$ ed è parallelo al vettore

{\begin{pmatrix}1\\f_{1}(t,x_{1},x_{2},\ldots ,x_{n})\\f_{2}(t,x_{1},x_{2},\ldots ,x_{n})\\\vdots \\f_{n}(t,x_{1},x_{2},\ldots ,x_{n})\end{pmatrix}}

Il numero, la posizione e la lunghezza dei segni di pendenza possono essere arbitrari. Le posizioni sono solitamente scelte in modo tale che i punti $(t,x_{1},x_{2},\ldots ,x_{n})$ creino una griglia uniforme. Il caso generale, descritto sopra, rappresenta $n=1$ . Il caso generale del campo di pendenza per sistemi di equazioni differenziali non è di facile visualizzazione $n>2$ .

Applicazione generale

Con i computer, è possibile creare campi di pendenza anche complicati molto rapidamente, e quindi un'applicazione pratica trovata solo di recente è quella di usarli per avere un'idea di quale dovrebbe essere una soluzione prima che venga cercata una soluzione generale esplicita. Naturalmente, i computer possono anche risolverne solo uno, se esiste.

Se non esiste una soluzione generale esplicita, i computer possono utilizzare i campi di pendenza (anche se non vengono visualizzati) per trovare numericamente soluzioni grafiche. Esempi di tali algoritmi sono il metodo di Eulero, o meglio, i metodi di Runge–Kutta.

Software per tracciare campi di pendenza

Diversi pacchetti software possono tracciare i campi di pendenza.

Codice del campo di direzione in GNU Octave / MATLAB

funn = @(x, y)y-x;               % function f(x, y) = y-x
[x, y] = meshgrid(-5:0.5:5);          % intervals for x and y
slopes = funn(x, y);              % matrix of slope values
dy = slopes ./ sqrt(1 + slopes.^2);      % normalize the line element...
dx = ones(length(dy)) ./ sqrt(1 + slopes.^2); % ...magnitudes for dy and dx
h = quiver(x, y, dx, dy, 0.5);         % plot the direction field
set(h, "maxheadsize", 0.1);          % alter head size

Esempio di codice per Maxima

/* field for y'=xy (click on a point to get an integral curve). Plotdf requires Xmaxima */ plotdf( x*y, [x,-2,2], [y,-2,2]);

Esempio di codice per Mathematica

(* field for y'=xy *)
VectorPlot[{1,x*y-5x},{x,-2,2},{y,-2,2}]

Esempio di codice per SageMath

^[4]

var('x,y')
plot_slope_field(x*y, (x,-2,2), (y,-2,2))

Esempi

y' = x/y
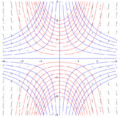Isocline (blu), campo di pendenza (nero) e alcune curve di soluzione (rosse)

Note

^ (EN) William Boyce e Richard-C DiPrima, Elementary Differential Equations and Boundary Value Problems, 7ª ed., Wiley, p. 3, ISBN 9780471319993.
^ (EN) Vladimir A. Dobrushkin, Applied Differential Equations: The Primary Course, Google libri, 2014, p. 13, ISBN 978-1-4987-2835-5. URL consultato il 15 luglio 2024.
^ (EN) Di Andrei D. Polyanin e Alexander V. Manzhirov, Handbook of Mathematics for Engineers and Scientists, CRC Press, 2006, p. 453, ISBN 978-1-58488-502-3. URL consultato il 18 luglio 2024.
^ (EN) Plotting fields, su doc.sagemath.org.