Problema del collezionista

Questa voce è orfana, ovvero priva di collegamenti in entrata da altre voci.

Inseriscine almeno uno pertinente e utile e rimuovi l'avviso. Segui i suggerimenti del progetto di riferimento.

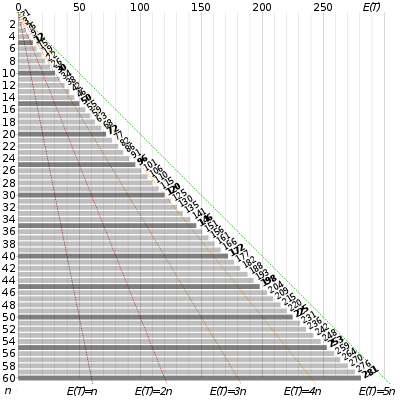
Il problema del collezionista (coupon collector's problem in inglese) è un problema di teoria della probabilità e calcolo combinatorio in cui un collezionista intende ottenere tutti gli oggetti di una data collezione (ad esempio, figurine), ma ha modo di espandere la propria raccolta solo tramite estrazioni casuali di un numero finito di copie dalla collezione originale (i pacchetti di figurine).

È possibile formulare il problema come segue: «Se un album contiene n figurine, quanti pacchetti di figurine vanno acquistati in media per poter completare l'album?». Oppure: «Dato un insieme di n elementi distinti, quante estrazioni con ripetizione si prevede di eseguire prima di aver estratto ogni elemento almeno una volta?».Na

Un'analisi formale del problema rivela che il numero atteso di tentativi necessari cresce secondo ${\displaystyle \Theta (n\log(n))}$^[1]. Ad esempio, per n = 50 ci vogliono 225^[2] tentativi per raccogliere tutte le 50 figurine.

Sia il tempo T il numero di estrazioni necessarie per ottenere tutte le n figurine, e sia t_i il tempo per trovare la i-esima figurina dopo aver raccolto i − 1 figurine. Allora ${\displaystyle T=t_{1}+\cdots +t_{n}}$. Si considerino T e t_i come variabili casuali . Si osservi che la probabilità di trovare una nuova figurina è ${\displaystyle p_{i}={\frac {n-(i-1)}{n}}={\frac {n-i+1}{n}}}$. Perciò, ${\displaystyle t_{i}}$ è una distribuzione geometrica con valore atteso ${\displaystyle {\frac {1}{p_{i}}}={\frac {n}{n-i+1}}}$. Per linearità del valore atteso, si ha:

${\displaystyle {\begin{aligned}\operatorname {E} (T)&{}=\operatorname {E} (t_{1}+t_{2}+\cdots +t_{n})\\&{}=\operatorname {E} (t_{1})+\operatorname {E} (t_{2})+\cdots +\operatorname {E} (t_{n})\\&{}={\frac {1}{p_{1}}}+{\frac {1}{p_{2}}}+\cdots +{\frac {1}{p_{n}}}\\&{}={\frac {n}{n}}+{\frac {n}{n-1}}+\cdots +{\frac {n}{1}}\\&{}=n\cdot \left({\frac {1}{1}}+{\frac {1}{2}}+\cdots +{\frac {1}{n}}\right)\\&{}=n\cdot H_{n}.\end{aligned}}}$

Qui, H_n è l'n-esimo numero armonico. Utilizzando l'analisi asintotica per i numeri armonici, si ottiene:

${\displaystyle \operatorname {E} (T)=n\cdot H_{n}=n\log n+\gamma n+{\frac {1}{2}}+O(1/n),}$

dove ${\displaystyle \gamma \approx 0.5772156649}$ è la costante di Eulero-Mascheroni.

Quindi, è possibile usare la disuguaglianza di Markov per delimitare l'intervallo di probabilità desiderato:

${\displaystyle \operatorname {P} (T\geq cnH_{n})\leq {\frac {1}{c}}.}$

Quanto sopra può essere modificato leggermente per gestire il caso in cui siano già state raccolte alcune figurine. Sia k il numero di figurine già raccolte, allora:

${\displaystyle {\begin{aligned}\operatorname {E} (T_{k})&{}=\operatorname {E} (t_{k+1}+t_{k+2}+\cdots +t_{n})\\&{}=n\cdot \left({\frac {1}{1}}+{\frac {1}{2}}+\cdots +{\frac {1}{n-k}}\right)\\&{}=n\cdot H_{n-k}\end{aligned}}}$

E per ${\displaystyle k=0}$, otteniamo il risultato di partenza.

Sfruttando l'indipendenza delle variabili casuali t_i, si ottiene:

${\displaystyle {\begin{aligned}\operatorname {Var} (T)&{}=\operatorname {Var} (t_{1}+\cdots +t_{n})\\&{}=\operatorname {Var} (t_{1})+\operatorname {Var} (t_{2})+\cdots +\operatorname {Var} (t_{n})\\&{}={\frac {1-p_{1}}{p_{1}^{2}}}+{\frac {1-p_{2}}{p_{2}^{2}}}+\cdots +{\frac {1-p_{n}}{p_{n}^{2}}}\\&{}<\left({\frac {n^{2}}{n^{2}}}+{\frac {n^{2}}{(n-1)^{2}}}+\cdots +{\frac {n^{2}}{1^{2}}}\right)\\&{}=n^{2}\cdot \left({\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+\cdots +{\frac {1}{n^{2}}}\right)\\&{}<{\frac {\pi ^{2}}{6}}n^{2}\end{aligned}}}$

poiché ${\displaystyle {\frac {\pi ^{2}}{6}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+\cdots +{\frac {1}{n^{2}}}+\cdots }$ (vedi problema di Basilea).

Quindi, è possibile usare la disuguaglianza di Čebyšëv per delimitare l'intervallo di probabilità desiderato:

${\displaystyle \operatorname {P} \left(|T-nH_{n}|\geq cn\right)\leq {\frac {\pi ^{2}}{6c^{2}}}.}$

È possibile derivare un limite superiore diverso a partire dalla seguente osservazione. Rappresentiamo con ${\displaystyle {Z}_{i}^{r}}$ l'evento per cui l'${\displaystyle i}$-esima figurina non è stata trovata nelle prime ${\displaystyle r}$ estrazioni. Allora:

${\displaystyle {\begin{aligned}P\left[{Z}_{i}^{r}\right]\leq \left(1-{\frac {1}{n}}\right)^{r}\leq e^{-r/n}\end{aligned}}}$

Pertanto, per ${\displaystyle r=\beta n\log n}$, si ottiene ${\displaystyle P\left[{Z}_{i}^{r}\right]\leq e^{(-\beta n\log n)/n}=n^{-\beta }}$.

${\displaystyle {\begin{aligned}P\left[T>\beta n\log n\right]=P\left[\bigcup _{i}{Z}_{i}^{\beta n\log n}\right]\leq n\cdot P[{Z}_{1}^{\beta n\log n}]\leq n^{-\beta +1}\end{aligned}}}$.

• Gunnar Blom, Lars Holst e Dennis Sandell, 7.5 Coupon collecting I, 7.6 Coupon collecting II, and 15.4 Coupon collecting III, in Problems and Snapshots from the World of Probability, New York, Springer-Verlag, 1994, pp. 85–87, 191, ISBN 0-387-94161-4..
• Brian Dawkins, Siobhan's problem: the coupon collector revisited, in The American Statistician, vol. 45, n. 1, 1991, pp. 76–82, DOI:10.2307/2685247, JSTOR 2685247..
• Paul Erdős e Alfréd Rényi, On a classical problem of probability theory (PDF), in Magyar Tudományos Akadémia Matematikai Kutató Intézetének Közleményei, vol. 6, 1961, pp. 215–220..
• Pierre-Simon Laplace, Théorie analytique des probabilités, 1812, pp. 194–195..
• Donald J. Newman e Lawrence Shepp, The double dixie cup problem, in American Mathematical Monthly, vol. 67, n. 1, 1960, pp. 58–61, DOI:10.2307/2308930, JSTOR 2308930.
• Philippe Flajolet, Danièle Gardy e Loÿs Thimonier, Birthday paradox, coupon collectors, caching algorithms and self-organizing search, in Discrete Applied Mathematics, vol. 39, n. 3, 1992, pp. 207–229, DOI:10.1016/0166-218X(92)90177-C..
• Richard Isaac, 8.4 The coupon collector's problem solved, in The Pleasures of Probability, Undergraduate Texts in Mathematics, New York, Springer-Verlag, 1995, pp. 80–82, ISBN 0-387-94415-X..
• Rajeev Motwani e Prabhakar Raghavan, 3.6. The Coupon Collector's Problem, in Randomized algorithms, Cambridge, Cambridge University Press, 1995, pp. 57–63, ISBN 9780521474658..

• Paradosso del compleanno

• Wikimedia Commons contiene immagini o altri file su Problema del collezionista

• "Coupon Collector Problem" di Ed Pegg, Jr., il Wolfram Demonstrations Project. Pacchetto per Mathematica.
• How Many Singles, Doubles, Triples, Etc., Should The Coupon Collector Expect?, una nota breve di Doron Zeilberger.