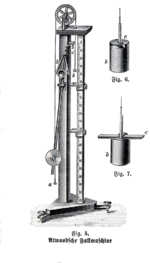
アトウッドの器械

古典力学
${\displaystyle {\boldsymbol {F}}={\frac {\mathrm {d} }{\mathrm {d} t}}(m{\boldsymbol {v}})}$ 運動の第2法則
歴史（英語版）
分野 静力学  · 動力学 / 物理学における動力学  · 運動学  · 応用力学  · 天体力学  · 連続体力学  · 統計力学 定式化 ニュートン力学 解析力学: ラグランジュ力学 ハミルトン力学 基本概念 空間 · 時間 · 速度 · 速さ · 質量 · 加速度 · 重力 · 力 · 力積 · トルク / モーメント / 偶力 · 運動量 · 角運動量 · 慣性 · 慣性モーメント · 基準系 · エネルギー · 運動エネルギー · 位置エネルギー · 仕事 · 仮想仕事 · ダランベールの原理 主要項目 剛体 · 運動 · ニュートン力学 · 万有引力 · 運動方程式 · 慣性系 · 非慣性系 · 回転座標系 · 慣性力 · 平面粒子運動力学 · 変位 · 相対速度 · 摩擦 · 単振動 · 調和振動子 · 短周期振動 · 減衰 · 減衰比 · 自転 · 回転 · 円運動 · 非等速円運動 · 向心力 · 遠心力 · 遠心力 (回転座標系) · 反応遠心力 · コリオリの力 · 振り子 · 回転速度 · 角加速度 · 角速度 · 角周波数 · 偏位角度 科学者 ニュートン · ケプラー · ホロックス · オイラー · ダランベール · クレロー · ラグランジュ · ラプラス · ハミルトン · ポアソン
表 話 編 歴

アトウッドの器械（アトウッドのきかい、英語: Atwood machine、Atwood's machine）とは、1784年にイギリス人数学者ジョージ・アトウッドによって発表された実験装置^[1]。この装置は一定加速度の運動を作る装置として発案され、当初はニュートン力学の法則を検証するために用いられたが、後には学校教育の中で法則を例示するために広く用いられるようになった^[2][3]。

理想的なアトウッドの器械は、 m₁ および m₂ の質量を持つ二つの物体を伸縮しない軽いひもでつなぎ、ひもを質量のない理想的な滑車にかけたものである^[4]。

m₁ = m₂ であるなら、おもりの位置によらずこの系は中立平衡の状態にある。 m₁ ≠ m₂ ならば、どちらの物体も等しい大きさの加速度を受ける。

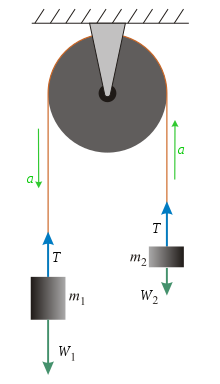
加速度についての方程式を作るには、この系に存在する力を数え上げる必要がある。ひもの伸縮と質量を無視し、また滑車は理想的であり質量を持たないとすれば、考慮すべき力はひもの張力（ T ）および各物体の重さ（ W₁ 、 W₂ ）のみである。それぞれの物体にはたらいている力を用いてニュートンの第二法則により運動方程式を立てれば、加速度（ a ）を含む連立方程式が得られる。

ここでは m₁ > m₂ として運動の方向を正の向きに取る。すなわち、 m₁ が下向き、 m₂ が上向きの加速度を持つとき a が正だと決める。重力加速度を g として、物体 m₁ 、 m₂ の重さはそれぞれ W₁ = m₁g および W₂ = m₂g である。

m₁ にはたらく力から運動方程式を立てると

${\displaystyle \;m_{1}g-T=m_{1}a}$

同様に、 m₂ にはたらく力から

${\displaystyle \;T-m_{2}g=m_{2}a}$

これらの二式を足し合わせると以下が得られる。

${\displaystyle \;m_{1}g-m_{2}g=m_{1}a+m_{2}a}$,

結局、加速度の式は次のようになる。

${\displaystyle a=g{m_{1}-m_{2} \over m_{1}+m_{2}}}$

上式を用いれば、逆に運動の加速度から g を求めることもできる。おもりの変位 d とともに時間 t を測定して

${\displaystyle d={1 \over 2}at^{2}}$.

の関係を用いれば a が得られ、さらに g を計算できる。

アトウッドの器械は運動方程式を導くラグランジュの方法を説明する題材として用いられることがある^[5]。

ひもの張力を求めたい場合、加速度の式

${\displaystyle a=g{m_{1}-m_{2} \over m_{1}+m_{2}}}$

をどちらかの運動方程式に代入する。たとえば m₁a = m₁g − T に代入すると

${\displaystyle T={2gm_{1}m_{2} \over m_{1}+m_{2}}={2g \over 1/m_{1}+1/m_{2}}}$

が導かれる。

m₁ と m₂ の間にわずかな差しかない場合には、滑車の慣性モーメント I が無視できなくなる。滑車の半径を r とすると、滑車とひもが互いに滑らないという条件のもとで、滑車の角加速度 α は以下で与えられる。

${\displaystyle \alpha ={a \over r}}$

トルクの合計 N_net を用いて α についての運動方程式を立てると

${\displaystyle {\begin{aligned}I\alpha &=N_{\mathrm {net} }\\&=\left(T_{1}-T_{2}\right)r-N_{\mathrm {f} }\\\end{aligned}}}$

N_f は摩擦によるトルクを表し、 T₁ と T₂ はそれぞれ m₁ 側と m₂ 側のひもの張力を意味する。上式をおもり二つの運動方程式と連立させ、 a 、 T₁ 、 T₂ について解くと

${\displaystyle a={{g(m_{1}-m_{2})-{N_{\mathrm {f} } \over r}} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}}$

${\displaystyle T_{1}={{m_{1}g(2m_{2}+{{I} \over {r^{2}}}+{{N_{\mathrm {f} }} \over {rg}})} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}}$

${\displaystyle T_{2}={{m_{2}g(2m_{1}+{{I} \over {r^{2}}}+{{N_{\mathrm {f} }} \over {rg}})} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}}$

滑車の軸受けでの摩擦が無視できる（が、滑車の慣性は無視できず、滑車とひもは互いに滑らない）場合には、上の三式は以下のように単純化される。

${\displaystyle a={{g(m_{1}-m_{2})} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}}$

${\displaystyle T_{1}={{m_{1}g(2m_{2}+{{I} \over {r^{2}}})} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}}$

${\displaystyle T_{2}={{m_{2}g(2m_{1}+{{I} \over {r^{2}}})} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}}$

アトウッドはロンドンの器具職人ジョージ・アダムス（英語版）に依頼してこの装置を作製させ、1770年に初めてトリニティ・カレッジ (ケンブリッジ大学) での講義に使用した^[3]。

オリジナルの装置には振り子時計が備えられており、運動の時間を計るために一定間隔の音が鳴るようになっていた。振り子の音とタイミングを合わせて、どちらかのおもりの上に制御棒（追加おもり）を載せることで運動が始まる。落下するおもりが小さな輪をくぐり抜けると、制御棒が輪に引っかかって取り除かれ、その後は加速度ゼロの運動が行われる。この速さを測ることで、おもりに加えられた加速を知ることができる。軸受で発生する摩擦を最小化するため滑車の車軸は4枚の車輪で支えられていた。過去に作製されたアトウッドの器械の多くがこの構造を踏襲している。^[1][3]

1780年代に王立協会のフェローで大陸の学会と関係が深かったJ・マジェラン（英語版）はアトウッドの器械を西欧各国に紹介した。このとき器械を入手したヴォルタはその精妙さに感嘆したという。19世紀になると、ロンドンやパリ、後にはアメリカの器具職人によって広く製造がおこなわれ、世界中に供給されるようになった。^[3]

つり合いおもりを備えたエレベーターは理想的なアトウッドの器械に近いため、巻き上げ機はかごの重量を上回る力を発生させる必要はない。かごとおもりの重量差および慣性に相当する力だけでよい。ケーブルでつながれた二台の車両が巻き上げ機によって斜面上を昇降するケーブルカーでも同じ原理が使われている。エッフェル塔のエレベーターは複数台がそれぞれ互いのつり合いおもりの役を果たしている。

• 重力加速度
• ケーターの振り子
• 球形の牛

• ケニオンカレッジ、グリーンスレード教授による解説記事（英語）
• "Atwood's Machine" by Enrique Zeleny、Wolframデモンストレーションプロジェクト。