メビウス変換
幾何学における平面上のメビウス変換(メビウスへんかん、英: Möbius transformation)は、
の形で表される複素一変数 z に関する有理函数である。ここで、係数 a, b, c, d は ad − bc ≠ 0 を満足する複素定数である。
幾何学的にはメビウス変換は、複素数平面を実二次元球面へ立体射影したものの上で回転と平行移動により各点の位置と向きを変更したものを再度平面に立体射影することによって得られる[1]。これらの変換は
メビウス変換は複素射影直線上の射影変換であり、その全体はメビウス群と呼ばれる射影一般線型群PGL(2, C) を成す。メビウス群およびその部分群は数学および物理学においてさまざまな応用を持つ。
メビウス変換の名はアウグスト・フェルディナント・メビウスの業績に因むものだが、ほかにも射影変換や一次分数変換(あるいは単に一次変換)などと呼ばれることもある。
概要
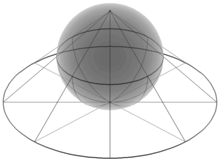
メビウス変換は通例、ガウス平面にただひとつの無限遠点を付け加えて得られる拡張複素平面 ˆC = C ∪ {∞} 上で定義されるものとして扱われる。拡張複素平面はリーマン球面と呼ばれる球面とみることもできるし、複素射影直線 CP1 とみることもできる。どんなメビウス変換も、リーマン球面からそれ自身への全単射な共形変換になり、また逆にそのような変換は実際にメビウス変換とならねばならない。
メビウス変換全体の成す集合は写像の合成を積として、メビウス群と呼ばれる群を成す。メビウス群は(リーマン球面をリーマン面とみなしたときの)リーマン球面上の自己同型群であり、しばしば Aut(ˆC) と記される。メビウス群は双曲的三次元空間上の向きを保つ等距変換全体の成す群に同型で、それゆえ双曲的三次元多様体の研究において重要な役割を演じる。
物理学においては、メビウス群がリーマン球面に作用するのと同じやり方で、ローレンツ群の単位成分が天球に作用する(実はこれらふたつの群は同型である)。相対論的速度にまで加速した観測者には、地球付近での見え方から無限小メビウス変換に従って連続的に変形された星座が見えているはずである。このような考察はしばしばツイスター理論の出発点として行われる。
メビウス群のいくつかの部分群は(ガウス平面や双曲平面などの)単連結リーマン面上の自己同型群を成す。そのような事情から、メビウス変換はリーマン面の理論においても重要な働きをする。どんなリーマン面の基本群もメビウス群の離散部分群となるのである(フックス群、クライン群など参照)。メビウス群の特に重要な離散部分群としてモジュラー群があり、それはフラクタルやモジュラー形式、楕円曲線あるいはペル方程式などといった多くの理論において中心的な役割を果たしている。
もっと一般に n > 2 なる次元を持つ空間においても、メビウス変換をn-次元超球面からそれ自身への向きを保つ全単射共形変換として定義することができる(そのような変換はその領域における共形変換のもっとも一般な形のものである)。共形写像に関するリウヴィルの定理(英語版)に従えば、メビウス変換は平行移動、相似変換、直交変換、反転の合成として表すことができる。
定義
メビウス変換の一般形は、a, b, c, d を ad − bc ≠ 0 を満たす任意の複素数として
で与えられる(ad = bc ならば、上記の有理函数は定数であって、メビウス変換とはみなされない)。c ≠ 0 の場合、これは
と定義することにより、リーマン球面全体まで拡張される。また、c = 0 ならば
と定義すれば、f(z) はリーマン球面からそれ自身への全単射な正則函数となる。
メビウス変換全体の成す集合は写像の合成に関して群を成す。上記の定義からメビウス函数の合成も反転も正則となり、この群には複素多様体の構造が与えられる。すなわち、メビウス群は複素リー群である。メビウス群は通例、リーマン球面の自己同型群と看做して と書かれる。
基本的な変換への分解とかんたんな性質
メビウス変換はもっと単純な変換の列に等価である。実際、
とおけば、これらの合成
はメビウス変換を与える。このようにメビウス変換を分解することで、メビウス変換のもつ多くの性質を浮き彫りにすることができる。メビウス逆変換の存在とその明示的な表示式は、この分解における単純な変換の逆変換を考えば、それらの合成を行うことによって直ちに導かれる。要するに、変換 g1, g2, g3, g4 を、各 gi が上記 fi の逆変換とすると、それらの合成
が、メビウス逆変換の式を与えるのである。
角の保存と広義の円
上述の分解から、円に関する反転 (circle inversion) についての非自明な性質がすべてメビウス変換にも遺伝していることが確認できる。たとえば、メビウス変換が等角写像となることは、反転以外の変換は拡大縮小と等距変換(平行移動、鏡映、回転)で明らかに角を保つので、円に関する反転が角を保つことの証明に帰着される。あるいはさらに、円に関する反転が広義の円を広義の円に写すことから、メビウス変換も同じ性質を持つ。ここで「広義の円」とは、直線については無限遠点を通る半径無限大の円と考えて円と直線をひとまとめに扱った概念である。メビウス変換によって狭義の円が直線に、直線が狭義の円に移ることもあり、必ずしも狭義の円が狭義の円に、直線が直線に写されるものとは限らないことに留意すべきである。また、円が円に移る場合においても、一方の円の中心が他方の円の中心に移るとは限らないことにも注意。
複比の保存
複比 (Cross-ratio) はメビウス変換で不変である。すなわち、メビウス変換が相異なる4つの点 z1, z2, z3, z4 を相異なる4つの点 w1, w2, w3, w4 にそれぞれ移すならば
が成立する。z1, z2, z3, z4 のうちの一点が無限遠点ならば、複比は自然な極限をとったものとして定義する。たとえば z1, z2, z3, ∞ の複比は
である。
射影行列表現
任意の 2 × 2 複素正則行列
に対して、メビウス変換
を対応させる。ad − bc ≠ 0 なる条件は、先の行列の行列式が 0 でない(つまり正則である)という条件と等価である。
ふたつの行列の積が対応するふたつのメビウス変換の合成に対応することは、直接計算で確かめることができる。言葉を変えれば、一般線型群 GL(2, C) からメビウス群への写像
は、群準同型を定めている。ここで注意すべきは を複素数 λ-倍して得られる行列はどれも同じメビウス変換に対応しているということであり、メビウス変換は対応する行列をそのようなスカラー倍の違いを除いて一意に決定するということである。すなわち、写像 π の核は単位行列 I のスカラー倍全体から成り、群の第一準同型定理から剰余群 GL(2, C)/(CI) がメビウス群に同型となることがわかる。さてこの剰余群は、一般射影線型群として知られ、通例 PGL(2, C) で表される。ここに、群の同型
が得られたことになる。同様にして任意の体 K 上で、射影線型群 PGL(2, K) と射影分数変換全体の成す群、あるいは射影直線を保つ射影線型自己同型全体の成す群とが同一視できる。これは、特に K が有限体のとき、代数学的に意味のある事実である。一方、複素数体の場合は幾何学的に非常に重要である。
PGL(2,C) による複素射影直線 CP1 への自然な作用は、射影直線 CP1 とリーマン球面とを
なる対応で同一視することにより、メビウス群のリーマン球面への作用にちょうど一致する。ここで、 [z1 : z2] は CP1 上の斉次座標であり、点 [1 : 0] がリーマン球面上の無限遠点 ∞ に対応する。
斉次座標を用いれば無限遠点 ∞ についての場合を分けて扱わずに済むので、メビウス変換に関する具体的な計算の多くが簡素化される。
上で、考える行列 を行列式が 1 のものに制限すれば、写像 を制限して特殊線型群 SL(2,C) からメビウス群への全射が得られる。この状況下での核は単位行列の ±1-倍のみから成り、したがって剰余群 SL(2, C)/{±I}(これを PSL(2, C) と書く)とメビウス群との同型
が得られる。このことから、メビウス群が 3-次元複素リー群(あるいは 6-次元実リー群)であることがわかる。これは半単純非コンパクトなリー群である。
任意に与えられたメビウス変換に対して、それを表現する行列式 1 の行列はちょうどふたつ存在する。つまり、SL(2, C) は PSL(2,C) の二重被覆である。また、SL(2, C) は単連結ゆえ、これはメビウス群の普遍被覆でもある。よって、メビウス群の基本群は Z2 であることがわかる。
メビウス変換は三点で決まる
リーマン球面上の相異なるみっつの点 z1, z2, z3 とさらに別の相異なるみっつの点 w1, w2, w3 が与えられたとき、zi をそれぞれ wi (i = 1, 2, 3) に写すメビウス変換 f(z) はただひとつ存在する(別な言いかたをすれば、メビウス群のリーマン球面への作用は鋭 3-重推移的である)。このように与えられた点集合からメビウス変換 f(z) を決定する方法がいくつか存在する。
初期値を 0, 1, ∞ に移す変換を用いる方法
行列
に対応するメビウス変換
が z1, z2, z3 をそれぞれ 0, 1, ∞ にそれぞれ写すことを確かめることは難しくない(zi の何れかが ∞ であるときは、それが ziなら上の式で全部の成分を先に zi で割っておいて zi → ∞ なる極限をとったものを として考える)。
同様に行列 を w1, w2, w3 をそれぞれ 0, 1, ∞ に写すようにとり、行列
を考えれば、z1, z2, z3 をそれぞれ w1, w2, w3 に写すメビウス変換が得られる。
明示的な行列式公式を利用する方法
方程式
は zw-平面における双曲線の標準形
と等価であるから、三つ組 (z1, z2, z3) を別の三つ組 (w1, w2, w3) へ写すメビウス変換 を構成する問題は、(zi, wi) (i = 1, 2, 3) を通る双曲線の係数 a, b, c, d を求める問題に等価である。このとき、明示的な方程式は行列式
を評価することによって求められる。この式を第 1-行の各成分を中心として余因子展開することにより得られる
を成分とする表現行列 が得られるが、このようにして得られた の行列式は
に等しく、これはまた zi がどのふたつも一致せず、かつ wi がどのふたつも一致しないならば 0 にはならないから、これによってメビウス変換がきちんと定まる。点 zi または wi の何れかが無限遠点 ∞ であるときは、先によっつの行列式をその変数で割ってからそれを ∞ に飛ばした極限を考えるものとする。
明示公式
明示公式は以下のようになる。
分類
恒等変換でないメビウス変換は一般に、抛物型、楕円型、双曲型と斜航型の4つのタイプに分類される(ただし、双曲型は斜航型の部分クラスである)。この分類は代数的な意味と幾何学的な意味の両方を備えている。幾何学的には、異なるタイプの変換はガウス平面上の変換として後で図示するような図形的な意味で異なる性質を示す。
これらのタイプは、トレース を見ることで判別することができる。トレースが共軛変換で不変、つまり
が成立すること、それゆえに同じ共軛類に属するどの元も同じトレースの値を持つことに注意する。如何なるメビウス変換も、その表現行列 が(適当に成分を定数倍することにより)行列式の値として 1 を持つようにすることができる。(何れも恒等変換でない)ふたつのメビウス変換 で
なるものが互いに共軛となるための必要十分条件は
が満たされることである。
以下の議論では、常に表現行列 が
に正規化されているものと仮定する。
抛物型変換
行列式 1 の行列 で定義される、恒等変換ではないメビウス変換が抛物型 (parabolic) であるとは、
であるときにいう(したがってトレースは ±2 のいずれかということになるが、与えられた変換に対して は符号の違いを除いて一意だから、何れか一方のみに決まる)。事実として、一方の選択肢では は恒等行列と同じ特性多項式 X2 − 2X + 1 を持ち、したがって冪単となる。メビウス変換が抛物型となるのは、それが拡張複素平面 C^ = C ∪ {∞} に唯一つの不動点を持つときであり、かつそのときに限る。そしてそのようなことが起きるためには、メビウス変換がガウス平面上の平行移動を定める行列
に共軛な行列によって定義されるものであることが必要十分である。
C^ に与えられた点を不動点として持つ抛物型メビウス変換の全体に恒等変換をあわせて考えた集合は、
の形の行列全体の成す群に同型な群を成す。これは(メビウス群の、あるいは線型代数群としての SL(2, C) の)ボレル部分群の冪単根基の例である(この概念は簡約リー群全般に対して定義される)。
特性定数
抛物型でない任意のメビウス変換は不動点をふたつ持ち、複素数 k = λ2 による乗法を通して拡大縮小・回転変換に対応する行列
に共軛な行列によって定義される。ここで複素数 λ は 0 でも ± 1 でもなく、メビウス変換の特性定数 (characteristic constant) または乗数あるいは倍率、比例定数 (multiplier) と呼ばれる。
楕円型変換
メビウス変換が楕円型 (elliptic) であるとは、その表現行列 のトレースが
なる実数となるときにいう。メビウス変換が楕円型となることと、上述の λ について |λ| = 1 となることとは同値である。いま、λ = eiα と書けば、α は実数であって、楕円型メビウス変換は
に共軛である。
特性定数 k を持つ如何なる についても、 の特性定数は kn となることに注意すべきである。このことから、有限位数のメビウス変換は必ず楕円型であり、λ は1の冪根とならねばならない。これはつまり、上述の α が π の有理数倍であるときに限るといっても同じことである。
双曲型変換
メビウス変換が双曲型 (hyperbolic) であるとは、それがトレースが実数である行列 で
なる条件を満たすものによって表現されるときにいう。メビウス変換が双曲型となるのは、λ が正の実数となるときであり、かつそのときに限る。
斜航型変換
メビウス変換が斜航型 (loxodromic) であるとは、 が [0, 4] に属さないときに言う。メビウス変換が斜航型となるための必要十分条件は、|λ| ≠ 1 となることである。
歴史的に、等角航路 (loxodrome) あるいは航程線 (rhumb line) に従った航行というのは一定の方角に航路をとることであった。この航跡は対数螺旋であり、斜航型メビウス変換がガウス平面に描く軌跡も同様である。変換の軌跡については後述。
一般の分類
| 変換 | トレースの平方 | 乗数 | 代表元 | |
|---|---|---|---|---|
| 楕円型 | ||||
| 抛物型 | ||||
| 双曲型 | ||||
| 斜航型 | ||||
実解析的な議論と語法についての注意
実変数に関する(もちろん係数も全て実数の)メビウス変換を考えれば、双曲型でない斜航型変換は存在せず、分類は(円錐曲線と同様に)楕円型、抛物型、双曲型の三種になる。この用語法は、トレースの絶対値の半分 |tr|/2 を変換の離心率として考えることによるものである。2 で割っているのは次元に対する補正であり、恒等変換が離心率 1 となるようにするものである(このような理由から、代わりに tr/n を考えることもある)。また、絶対値をとるのは作用が PSL において ±1 の因子を除いて定まることに対する補正である。あるいはまた、先に述べたと同様に離心率の平方の代わりとしてトレースの平方の半分を用いることもある。これらの分類は(平方を取るのと絶対値を取るのとでは値が違うから、完全に離心率を与えるわけではないけれども)実トレースの場合は一致し、複素トレースの場合には一致しない。同じ用語法が SL(2, R) の元の分類に対しても用いられ、また別のところでも類似の分類が用いられる。斜航的変換は本質的に複素解析的な現象であり、複素的な離心率に対応するものである。
不動点
恒等変換ではない任意のメビウス変換はリーマン球面上にふたつの不動点 γ1, γ2 を持つ。ただし、ここでふたつというのは重複度まで込めてふたつという意味である(つまり、抛物型変換についてはふたつの不動点が重なっているものと考える)。ふたつのうちの一方あるいは両方の不動点が無限遠にあってもよい。
不動点の決定
メビウス変換
の不動点は不動点方程式 f(γ) = γ を解くことで得られる。c ≠ 0 のとき展開して整理して得られる二次方程式
からふたつの根、つまり変換の不動点
は直ちに得られる。変換が抛物型なら (a + d)2 = 4(ad − bc) で不動点が一致することに注意する。また判別式は
となる。c = 0 の場合は二次方程式は一次方程式に退化してしまうが、これは不動点が無限遠にある状況に対応している。このときさらに a ≠ d ならもう一方の不動点は有限であり、
で与えられる。この場合のメビウス変換は、平行移動と回転変換および拡縮変換の合成として
で与えられる単純な変換になる。いっぽう、c = 0 かつ a = d の場合は不動点がふたつとも無限遠にあるときで、メビウス変換が純粋な平行移動として
なる形に表される状況に対応している。
位相幾何学的な証明
位相幾何学的には、(恒等変換でない)メビウス変換が 2-点を固定するという事実は
つまり、(リーマン)球面のオイラー標数が 2 であることに対応している。まず、射影線型群 PGL(2, K) の作用は単純 3-推移的である(3-点の順序三つ組がふたつ与えられれば、その一方を他方へ写す写像はただひとつメビウス変換として定まる)ことが代数的に(この群は 3-次元なので、本質的に次元の勘定(英語版)で)証明される。したがって、少なくともみっつの点を固定するようなメビウス変換は、恒等変換以外には無い。
つぎに、メビウス群は連結ゆえ任意のメビウス変換は恒等変換にホモトピックである。レフシェッツ-ホップの定理の述べるところによれば、高々有限個の不動点を持つ写像の不動点の指数(index; ここでは重複度のこと)の総和は写像のレフシェッツ数に等しい。この数はこの場合、ホモロジー群上の恒等写像のトレースであり、単純にオイラー標数と一致する。
これに対して、実数直線上の射影線型群 PGL(2, R) の作用は不動点を持つとは限らない。たとえば (1 + x)/(1 − x) は実数直線上に不動点を持たない(複素変換としてならば ±i を固定する[note 1])が、写像 2x は 0 と ∞ のふたつの点を固定する。これは円(実射影直線)のオイラー標数が 0 であり、したがってレフシェッツの不動点定理の主張が不動点の数は少なくとも 0 個なければならない(もちろん 0 個より多くてもよい)こと意味することに対応している。
正規形
メビウス変換をその不動点を用いた正規形 (normal form) と呼ばれる形に表すこともある。まずは相異なるふたつの不動点をもつ非抛物型の場合を考えよう。
非抛物型の場合
非抛物型のメビウス変換は、複素数 k によって
の形に表される変換(0 と ∞ が不動点)である回転・拡縮と共軛である。いま、γ1, γ2 を有限と仮定すれば、写像
は (γ1, γ2) を (0, ∞) に移す。一方が既に無限遠にある場合には、その無限遠点は固定して他方を 0 に送るように g を修正する。
f が相異なる不動点 γ1, γ2 を持つならば、変換 gfg−1 は 0 および ∞ を不動点に持ち、したがってそれは回転・拡縮変換
となることがわかる。したがって変換 f の不動点方程式は
と書くことができる。これを f について解いたものは(行列の形で書けば)
あるいは、不動点の一方が無限遠にあるときは
となる。上述の式から、不動点における f の微分係数を
と計算することができる。ふたつの不動点に順序付けが与えられれば、f の乗数の一方 (k) をf の特性定数として区別することができることに注目しよう。
であり、不動点の順序を入れ替えることは乗数の逆数を特性定数として選ぶことに相当する。
斜航型変換については、|k| > 1 なるときは常に、γ1 を反発的 (repulsive) 不動点、γ2 を吸引的 (attractive) 不動点と呼ぶ。|k| < 1 のときは役割が逆になる。
抛物型の場合
メビウス変換 f が抛物型の場合は、不動点 γ はただひとつである。この点を ∞ へ移す変換は
あるいは、γ 自身が無限遠点のときは恒等変換であり、変換 gfg−1 は無限遠点を固定するので、平行移動
となる。β はこの平行移動の長さあるいは移動距離 (translation length) と呼ばれる。したがって、抛物型変換の不動点公式は
であり、これを f について解いて(行列の形に書けば)
あるいは、γ = ∞ のときは
を得る。ここで、β は f の特性定数ではないことに注意すべきである(抛物型変換の特性定数は常に 1 である)。得られた式から、f′(γ) = 1 がわかる。
特性定数の幾何学的解釈
特性定数はその対数を考えることによってその性質を分類することができる。すなわち、
とおくとき、実数 ρ はスケールファクタであり、不動点 γ1 からどれほど反発的か、および不動点 γ2 にどれほど吸引的かを指し示す。また実数 α は回転因子であり、この変換で不動点 γ1 の周りを反時計回りに、不動点 γ2 の周りを時計回りに、どれだけ回転するかを指し示す。
楕円型変換
ρ = 0 の場合、不動点は反発的でも吸引的でもなく中立的であり、そのような変換は楕円型であるという。楕円型変換では任意の点が二つの不動点の周りをまわる円に沿って動く。一方の不動点が無限遠の場合は、これは一点の周りのアフィン回転を行うことと同値である。
任意の楕円型メビウス変換で生成される一径数部分群をとれば、この部分群の各変換が同じ二点を固定するような、連続変換が得られる。他の点はどれもリーマン球面上の二つの不動点の間でネストされた円の族に沿って流れる。一般に、二つの不動点は相異なる任意の二点を取ることができる。
このことは重要な物理学的解釈を持つ。観測者がある軸に関して角速度一定の回転をすることを想像し、二つの不動点を天球の北極と南極にとることにすれば、夜空の様子はちょうど二つの不動点 0, ∞ を共有する楕円型変換全体の成す一径数部分群によって記述されるのと同じ仕方で連続的に変換される。実数 α は観測者の一定な角速度に対応する。
次の二つの図は、楕円型メビウス変換のリーマン球面への効果(を平面へ立体投影したもの)を表したものである。
 |
 |
これらの図は単独のメビウス変換の効果を図示したものである。一径数部分群は、これを図によって示唆される円弧の族に沿って各点を「連続的に」動かすことで生成される。
双曲型変換
α が 0(または 2π の整数倍)ならば、その変換は双曲型であるという。双曲型変換では、各点は不動点の一方から他方へ円軌道に沿って動く。
任意の双曲型メビウス変換で生成される一径数部分群をとれば、この部分群の各変換が同一の二点を不動にするような、連続変換が得られる。不動点以外の点は一方の不動点から出て他方の不動点へ向かう円弧の族に沿って流れる。一般に、二つの不動点はリーマン球面上の相異なる任意の二点にとりうる。
これにも重要な物理的解釈がある。観測者が天球上の北極へ向かって加速度一定で加速する場合を考えると、夜空の様子は 0, ∞ を共通の二つの不動点とする双曲型変換全体の成す一径数部分群によって記述される仕方と全く同じように変化する。ここで実数 ρ は観測者の加速度の大きさに対応する。夜空の星は黄経に沿って南極から北極へ向けて動くように見える(黄経は球面から平面への立体射影で写せば円弧として見える)。
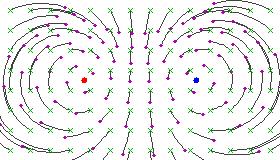
以下は双曲型メビウス変換がリーマン球面上へ与える効果(を平面に立体射影したもの)を図示したものである。

この図は、円弧的流線が二つの不動点の間で一定の角を内在するから、不動点に負の電荷を置いたときの電気力線の様子と似ている。
斜航型変換
ρ も α も 0 でないときは、その変換は斜航型であるという。斜航型変換では、各点は一方の不動点から他方の不動点へSの字の軌道を描いて動く。
「斜航」(loxodrome=航程線)の原義はギリシア語: λοξος(斜めの)+ ギリシア語: δρόμος(行程)である。一定方角を保つ航行を行うとき、例えば北西に進路を保つとすると、航路は対数螺旋を描いて北極の周りを無限に巻いていくものになる。メルカトール図法ではこの航路は、北極と南極を無限遠に射影するとき、直線になる。この経線に対する内在的な斜航角(つまり傾き、あるいは螺旋の巻きの「緊さ」)は、特性定数 k の偏角である。もちろん、北極と南極だけではなくて、メビウス変換はその二つの不動点をどこにでも設定できるけれども、任意の斜航型変換による各点の動きはこの斜航線に沿って各点が動く変換と必ず共軛になる。
任意の斜航型メビウス変換で生成される一係数部分群をとれば、この部分群の各変換が同じ二点を固定するような、連続変換が得られる。固定されない点は全て、一方の不動点から出て他方の不動点へ入るようなある曲線族に従って移動する。これが双曲型の場合と異なるのは、その曲線が円弧ではなくて、リーマン球面から平面への立体射影で写すと、一方の不動点を反時計回りに、他方の不動点を時計回りにそれぞれ無限回廻る、ひねられた螺旋となるような曲線になっていることである。一般に、二つの不動点はリーマン球面の相異なる任意の二点がとれる。
この場合も、二つの不動点が 0 と ∞ であるならば物理的解釈が可能である。観測者がある軸に関して角速度一定で回転しつつ同軸上を一定の速度で移動するものとすれば、このときの夜空の様子は 0 と ∞ を不動点とする斜航型変換全体の成す一径数部分群に従って変化する。実数 ρ および α はそれぞれ軸上の移動速度と軸周りの角速度の大きさを定める。
立体射影
以下の図は、メビウス変換がリーマン球面の上への立体射影であることを示すものである。球面の上への射影をするとき、不動点が無限遠にある特別の場合には、任意の場所に不動点を持つ場合と何も違わないように見えることに特に注意。
| 一方の不動点が無限遠にある場合 | ||
 |  |  |
| 二つの不動点が対蹠の位置にある場合 | ||
 |  |  |
| 不動点が任意の場所にある場合 | ||
 |  |  |
変換の反復適用
メビウス変換 が不動点 γ1, γ2 と特性定数 k を持つならば、同じ変換の反復合成変換
は不動点 γ′1 = γ1, γ′2 = γ2 と特性定数 k′ = kn を持つ。このことは、反復合成を各段階に分けて図示するときにも利用できる。
変換の極
メビウス変換 によって無限遠点 ∞ へ移される点
は変換 の極 (pole) と呼ばれる。また、無限遠点 ∞ が によって移る点
をしばしば逆極 (inverse pole) と呼ぶ。メビウス変換がひとつ与えられると、この二種類の極の中点は必ずその変換のふたつの不動点の中点にもなっており、したがって
なる関係式が成立する。これらよっつの点を頂点として平行四辺形が形成され、それをしばしばメビウス変換の特性平行四辺形 (characteristic parallelogram) などと呼び表す。
メビウス変換 をそのふたつの不動点 γ1, γ2 と極 z∞ を指定することによって特定することもできる。実際、行列
で与えられる変換は、γ1, γ2 を不動点に持ち、z∞ を極とする変換になる。このようにすれば、不動点 γ1, γ2 が与えられたとき、乗数 k と極 z∞ の間の変換則として
が得られる。これを成分を用いて書き下せば、
となるが、この最後の式はメビウス変換を表す行列
の固有値比 λ1/λ2(どちらの固有値を分母にするかで、それらの比は互いに逆数の関係にあるふたつを考えることができるが、そのうちのひとつ)に一致している(先の特性定数に関する節における議論と比較せよ)。実際、この行列の特性多項式は
となり、これは
を根に持つ。
ローレンツ変換
実ミンコフスキー空間は、実数の順序四つ組 (x0, x1, x2, x3) 全体からなる四次元座標空間 R4 に二次形式
をあわせて考えたものである。特殊相対論の用語を借りれば、Q > 0 となる点は時間的 (timelike) であると考えられ、さらに x0 > 0 となる点は未来方向 (future-pointing) であるという。また、Q < 0 となる点は空間的 (spacelike) であるという。零錐 (null cone) S は Q = 0 なる点全体の成す集合をいい、未来方向零錐 (future null cone) N+ は零錐の中でも x0 > 0 なる点全体から成る。したがって、天球は R4 の原点を始点とする N+ 内の半直線全体の成す集合と同一視される。行列式が正で二次形式 Q と時間方向を保つ R4 上の線型変換全体の成す集合は制限ローレンツ群 SO+(1, 3) を成す。
天球の幾何学に関して、その変換群 SO+(1, 3) はスピノル上のスピン群の作用を見ることにより、メビウス変換の群 PSL(2, C) と同一視される (Penrose & Rindler 1986)。各 (x0, x1, x2, x3) ∈ R4 に対して、エルミート行列
を対応させれば、この行列 X の行列式は二次形式 Q(x0, x1, x2, x3) に等しい。このような行列全体の成す空間には、特殊線型群 SL(2, C) がその各元 A に対して
となるものとして作用する。det A = 1 であるから、SL(2, C) のこの作用は X の行列式を保つ。ゆえに、X の行列式と二次形式 Q との同一視を通して、SL(2, C) の各元はローレンツ変換として作用している。次元的な理由で SL(2,C) は SO(1, 3) の近傍を被覆するが、SL(2, C) は連結ゆえ、制限ローレンツ群 SO+(1, 3) の全体を被覆する。さらにいえば、上で与えた作用の核が {±I} なる部分群ならば、商をとることで群の同型
が得られる。(x0, x1, x2, x3) がヌル、つまり行列 X の行列式が 0 であり、したがって複素二次元のベクトル ξ とその複素共軛によって
と直積に分解される場合に注意を向けよう。二次元ベクトル ξ には SL(2, C) が上で与えた作用と両立するような仕方で作用する。ここで、エルミート行列からなる空間における SL(2, C) の表現の核が {±I} となることは明らかである。
PSL(2, C) の天球への作用も立体射影を用いて幾何学的に記述することができる。まずは、x0 = 1 で与えられる R4 内の超平面を考え、その超平面と未来方向零錐 N+との交わりとして得られる球面 S+ と天球とを同一視する。この球面の北極 (1,0,0,1) から平面 x3 = 0 の上への立体射影は、x12 + x22 + x32 = 1 とするとき、
- (1, x1, x2, x3)
なる座標を持つ点を
へ写す。
複素座標函数
を導入すれば、この立体射影の逆変換は S+ 上の各点 (x1, x2, x3) に対して
なる式で与えられる。N+ への SO+(1,3) の作用は超平面 S+ を保たないが、S+ の各点について(N+ の点と思って)作用させたものを、その移動先が再び S+ に属するように再スケールしてやることで、SO+(1, 3) を複素変数 ζ への作用まで込めて球面 S+ に作用させることができる。天球のこの表現から調べるのは用意ではないが、実はこの作用は一次分数変換による作用になっている。逆に、複素変数 ζ に関する任意の一次分数変換を、適当な(一意的に決まる)再スケールを施すことになるかもしれないが、一意的に N+ 上のローレンス変換にすることができる。
立体射影の記述をなるべく変えずにより作用が見やすくなるようにするには、変数 ζ = z : w を複素射影直線 CP1 に対する斉次座標の対の比と考えることである。この立体射影は、C2 − {0} から N+ への実スケールに関して斉二次の変換
にすることができて、これは zz + ww = 1 なるスケールに制限すれば、上で述べた対応に一致する。この式の各成分はちょうど、直積
から得られる。まとめると、制限ローレンツ群 SO+(1,3) の作用はメビウス群 PSL(2, C) のそれと一致する。このことは、以下の定義の動機付けになっている。n ≥ 2 に対して、
- n-次元メビウス群 Möb(n) とは、n-次元球面 Sn からそれ自身への向きを保つ共形等距変換全体の成す群のことである。
ミンコフスキー空間 R1,n+1 内の零錐の未来方向半直線全体の成す空間として共形球面を実現することにより、Möb(n) と、行列式が正で時間方向を保つローレンツ変換全体の成す制限ローレンツ変換群 SO+(1, n + 1) との間に同型が存在する。
双曲空間
既に見たように、メビウス群 PSL(2,C) はミンコフスキー空間に原点、空間の向き、時間方向を全て保存する等距変換全体の成す群として作用する。また、この作用を正光錐における Q = 1 なる点の全体(これは三次元双曲空間 H3 のモデルを為す)に制限することにより、メビウス群を各元が H3 に向きを保つ等距変換として作用する群として捉えることができる(実際には、メビウス群と三次元双曲空間上の向きを保つ等距変換全体の成す群とは一致する)。
ポアンカレ球体模型を用いて、R3 における単位球体と H3 とを同一視するならば、リーマン球面を H3 の「共形的境界」として考えることができる。これにより、どのような H3 の向きを保つ等距変換からでもリーマン球面上のメビウス変換がえられ、逆にメビウス変換から向きを保つ等距変換もまた同様に得られる。このことは、物理学におけるAdS/CFT対応予想へ至るまさにその最初の所見である。
メビウス群の部分群
メビウス変換の係数 a, b, c, d が ad − bc = 1 を満たす実数である場合を考えると、PSL(2, R)で表されるメビウス群の部分群が得られる。この群は、上半平面 H = {x + iy | y > 0} をそれ自身へ写すメビウス変換全体の成す群であり、また H から H への双正則(あるいは同じことだが、全単射等角かつ向きを保つ)変換全体の成す群である。上半平面に計量を導入して、双曲平面 H2 の模型(ポアンカレ平面模型と呼ばれるもの)にすることができるが、このとき PSL(2, R) はこの模型において H2 の向きを保つ等距変換全体の成す群に等しい。
開円板 D = {z | |z| < 1} をそれ自身に写すメビウス変換全体の成す部分群は、φ ∈ R, b ∈ C, |b| < 1 なる定数によって得られる
なる形の変換全体から成る。これはまた、D から D への双正則(あるいは同じことだが、全単射、等角かつ向きを保つ)変換全体の成す群にも等しい。適当な計量を入れることにより、D はポアンカレ円板模型と呼ばれる先程のものとは異なる双曲平面の模型にすることができるが、この群は、この模型における H2 の向きを保つ等距変換全体の成す群に一致する。
本節に述べたふたつの部分群は、何れも H2 の等距変換群としてえられるから、これらは互いに同型である。具体的な同型写像は、開円板を上半平面に全単射に写す変換
と共軛変換によって得られる。
メビウス群 の極大コンパクト部分群は
で与えられる[2]。この部分群は、同型 を通じて、射影特殊ユニタリ群 PSU(2, C) に同型で、この群は 3-次元における回転全体の成す群である特殊直交群 SO(3) にも同型なので、メビウス群の極大コンパクト部分群をリーマン球面における回転全体の成す群として解釈することができる。任意の有限部分群は共軛変換でこの極大コンパクト部分群の中に写され、それゆえそれらの群はちょうど多面体群、三次元における点群に対応する。
メビウス変換からなる正二十面体群(英語版)はクラインによって (Klein 1888) において五次方程式の解析解を与えるために用いられた(現代的な解説が (Tóth 2012) にある[3])。
さて、メビウス変換の係数 a, b, c, d を ad − bc = 1 なる整数と仮定するならば、モジュラー群 PSL(2, Z) と呼ばれる PSL(2, R) の離散部分群で、ガウス平面上の格子および、楕円函数、楕円曲線の研究において重要な群を生じる。PSL(2, R) の離散部分群はフックス群として知られ、リーマン面の研究において重要である。
関連項目
脚注
注釈
出典
参考文献
- Arnold, Douglas N.; Rogness, Jonathan (November 2008), “Möbius Transformations Revealed”, Notics of AMS 55 (10): 1226-1231, http://www-users.math.umn.edu/~arnold/papers/moebius.pdf
- Beardon, Alan F. (2012) [1983], The Geometry of Discrete Groups (Softcover reprint of the original 1st ed.), New York: Springer-Verlag, ISBN 978-1-4612-7022-5
- Jones, Gareth A.; Singerman, David (1987), Complex Functions: an Algebraic and Geometric Viewpoint, Cambridge: Cambridge University Press, ISBN 978-0-521-31366-7 - ガロア群として見たローレンツ群とその同型に関しては第2章を参照。
- Hall, G. S. (2004), Symmetries and Curvature Structure in General Relativity, Singapore: World Scientific, ISBN 981-02-1051-5 - ローレンツ群のリー代数におけるリー部分代数および共役に関する類別に関しては第6章を参照。
- Katok, Svetlana (1992), Fuchsian Groups, Chicago:University of Chicago Press, ISBN 978-0-226-42583-2 - 第2章を参照。
- Klein, Felix (2003) [1888], Lectures on the ikosahedron and the solution of equations of the fifth degree, Dover Publication, ISBN 978-0-486-49528-6, http://digital.library.cornell.edu/cgi/t/text/text-idx?c=math;cc=math;view=toc;subview=short;idno=03070001
- Knopp, Konrad (2016) [1952], Elements of the Theory of Functions, New York: Dover Publication, ISBN 978-0-486-60154-0 - リーマン球面・立体射影・メビウス変換に関する美しい導入方法についてはこの古典的書籍の第3章から第5章を参照。
- Mumford, David; Series, Caroline; Wright, David (2015) [2002], Indra's Pearls: The Vision of Felix Klein, Cambridge University Press, ISBN 978-1-107-56474-9 - 非数学者向け。図形のイラストが豊富で、理論と結果に関する優れた解説を提供している。
- マンフォード, D.、シリーズ, C.、ライト, D. 著、小森洋平 訳『インドラの真珠 クラインの夢みた世界(英語版)』日本評論社、2013年3月。ISBN 978-4-535-78361-4。
- Needham, Tristan (1999) [1997], Visual Complex Analysis, Oxford: Clarendon Press, ISBN 978-0-19-853446-4 - メビウス変換とその共役に関する類別を含み、美しいイラストがある導入については第3章を参照。
- Penrose, Roger; Rindler, Wolfgang (1987), Spinors and space-time, Volume 1: Two-spinor calculus and relativistic fields, Cambridge University Press, ISBN 978-0-521-33707-6
- Tóth, Gábor (2012) [2002], Finite Möbius groups, minimal immersions of spheres, and moduli, Springer, ISBN 978-1-4612-6546-7
関連文献
- Lawson, M. V. (1998). “The Möbius Inverse Monoid”. Journal of Algebra 200 (2): 428. doi:10.1006/jabr.1997.7242.
外部リンク
- A java applet allowing you to specify a transformation via its fixed points and so on[リンク切れ].
- A java applet demonstrating iterated application of a Möbius transformation to a circle[リンク切れ].
- Conformal maps gallery
- Weisstein, Eric W. "Linear Fractional Transformation". mathworld.wolfram.com (英語).
- Möbius Transformation Module by John H. Mathews
- Linear Fractional Transformations at MathPages
- Möbius Transformations Revealed, by Douglas N. Arnold and Jonathan Rogness (a video by two University of Minnesota professors explaining and illustrating Möbius transformations using stereographic projection from a sphere). A high resolution version in QuickTime format is available at http://www.ima.umn.edu/~arnold/moebius/index.html .

















![{\displaystyle [z_{1}:z_{2}]\leftrightarrow z_{1}/z_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c07435882ec34c4a19905e6ec33b81d34362997e)















































![{\displaystyle \sigma \in \mathbb {C} ,\sigma \not \in [0,4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15000bbdc1fdc0f21ce7e23d7400283d5de6810b)






















































