| 円周率 |
|---|
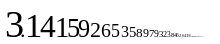 |
| 使用 |
|---|
| |
| 特性 |
|---|
| |
| 数値 |
|---|
| |
| 人物(日本人) |
|---|
| |
| 人物 |
|---|
| |
| 歴史 |
|---|
| |
| 文化 |
|---|
| |
| 関連項目 |
|---|
| |
|
円周率の無理性の証明(えんしゅうりつのむりせいのしょうめい)は、円周率が無理数であること、すなわち円周率の小数展開が無限に続き、しかも循環しないことの証明である。円周率が無理数であること自体はよく知られた事実であるが、その証明を目にする機会はあまりない[1]。知られている中で最も簡単な証明は、初等的な微分積分学のみを用いるものである。
歴史
円周率は古代から考察の対象とされ、無理数であることは紀元前4世紀のアリストテレスが予想していたが、証明されたのは二千年以上後のことである。1761年、ドイツの数学者ヨハン・ハインリッヒ・ランベルトは、正接関数の無限連分数表示

を用いて、初めて円周率の無理性を示した[2]。その証明は現代的にはやや不満の残るものであったが、1794年にフランスのアドリアン=マリ・ルジャンドルは厳密な証明を与え、さらに π2 も無理数であることを発見した。したがってルジャンドルは π の無理性よりも強い結果を示した。
20世紀には、初等的な微分積分学の知識のみを用いた証明が発見された。そのうち最もよく知られたものは、カナダ出身のイヴァン・ニーベンが1947年に発表した証明[3]である。それ以前の1945年にも、イギリスのメアリー・カートライト(英語版)が似た証明を与えている。彼女はそれを公表しなかったが、後にハロルド・ジェフリーズの著書に収録された[4]。1949年、日本の岩本義和は、ニーベンのアイデアを用いて π2 が無理数であることの初等的な証明を与えた[5]。
1978年、フランスのロジェ・アペリーは全ての立方数の逆数和

が無理数であることを示した(アペリーの定理を参照)。この値は、リーマンゼータ函数

の s = 3 における値 ζ(3) である。同様の手法で、彼は全ての平方数の逆数和

すなわち ζ(2) も無理数であることを示した。この極限は  に等しい、という事実をすでにレオンハルト・オイラーが示していたので(バーゼル問題を参照)、これはルジャンドルが示したことと同値である。すなわち、アペリーの証明は π2 が無理数であることの別証明になっている。
に等しい、という事実をすでにレオンハルト・オイラーが示していたので(バーゼル問題を参照)、これはルジャンドルが示したことと同値である。すなわち、アペリーの証明は π2 が無理数であることの別証明になっている。
証明
本節では、ニーベンの証明を紹介する。原論文は必要最低限の記述しかないが、ここではいくらか解説を加えている。円周率 π は、正弦関数 sin x の正の零点の中で最小のものとする[6]。証明は背理法による。すなわち π が有理数であり  (a, b は正の整数)と表せるものと仮定して、それから矛盾を導く。
(a, b は正の整数)と表せるものと仮定して、それから矛盾を導く。
自然数 n に対して、実関数 fn(x) を

で定義する。さらに、

とおく。ここで、f(k) は f の k 階微分を表す。
補題 1:Fn(0) は整数である。
証明:fn(x) の定義式を二項展開すると、

fn(k)(x) に x = 0 を代入することを考える。
k < n のときは、fn(k)(x) の各項は全て1次以上だから、fn(k)(0) = 0。
n ≤ k ≤ 2n のときは、x = 0 を代入する際に、1次以上の項は同様に 0 となるため、定数項のみが残り、

となる。
n ≤ k ≤ 2n より  , a2n−k, bk−n は整数であるから、fn(k)(0) は整数である。
, a2n−k, bk−n は整数であるから、fn(k)(0) は整数である。
ゆえに、fn(k)(0) の和・差である Fn(0) は整数である。
補題 2:Fn(π) = Fn(0)
証明: より fn(π − x) = fn(x) 、この両辺を k 階微分すると、連鎖律(合成関数の微分法則)より、
より fn(π − x) = fn(x) 、この両辺を k 階微分すると、連鎖律(合成関数の微分法則)より、

が(正確には数学的帰納法により)分かる。k = 0, 2, 4, …, 2n を代入して得られる式の総和を取ると、

を得る。x = 0 を代入すると、補題の式が得られる。
補題 3:
証明:deg fn = 2n より fn(2n+2)(x) = 0、ゆえに、

これと、積の微分法、三角関数の微分の公式(微分法#概要参照)を用いると、

を得る。微分積分学の基本定理より、
![{\displaystyle \int _{0}^{\pi }f_{n}(x)\sin x\,dx={\bigg [}F'_{n}(x)\sin x-F_{n}(x)\cos x{\bigg ]}_{0}^{\pi }=F_{n}(\pi )+F_{n}(0)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25ac72a5cd8c10484999e764e3e33690e5f6ce81)
となる。最後の等式では、π が正弦関数の零点であることを用いた。補題 2 より、これは 2Fn(0) に等しい。
結び: 0 < x < π の範囲では fn(x) > 0 かつ sin x > 0 である(π は正弦関数の正の零点のうち「最小の」ものであることに注意)。ゆえに、fn(x) sin x > 0, 補題 3 より Fn(0) > 0 である。次に、この Fn(0) を上から評価する。

より、

を得る。0 ≤ x ≤ π で 0 ≤ sin x ≤ 1、補題 3 より、

ここで、自然数 n は任意である。一般に、 が成り立つ。したがって、十分大きな n に対して 0 < Fn(0) < 1 が成り立つ。これは補題 1 に矛盾する。(証明終)
が成り立つ。したがって、十分大きな n に対して 0 < Fn(0) < 1 が成り立つ。これは補題 1 に矛盾する。(証明終)
カートライトの証明
ハロルド・ジェフリーズは、この証明法はメアリー・カートライト(英語版)が1945年にケンブリッジ大学の試験問題として出したもので,彼女はそれをどこからとったのかを明らかにしていないと書いている(注:証明の詳細については英語版の記述を見られたい)。
 と置き、自然数 n に対し、
と置き、自然数 n に対し、

と置く。このとき、 は整数となる。また、十分大きな n に対し、
は整数となる。また、十分大きな n に対し、 が言える。これらは矛盾する。
が言える。これらは矛盾する。
L. Zhou と L. Markov の証明
ニーベン・インケリの定理より、s2 が 0 でない有理数ならば、cos s は無理数である。cos π = −1 は有理数であるから、π2 ≠ 0 は無理数である[7](したがって π も無理数である)。
Zhou–Markov は π が無理数であることの別の初等的な証明も与えている[7]。
ニーベン・インケリの定理の証明を次に示す[7]。
整数 n ≥ 0 に対して

とおき

とおく。n = 0 のときの積分をすると

である。各積分を1回ずつ部分積分することにより、n > 0 に対して次の漸化式を得る。

これらより、I n , J n , K n , L n は、すべて

の形になる。ただし、u n ( R ) と v n ( R ) は整数係数の R = r 2 の多項式で、次数は高々 2 n + 1 である。

だと仮定すると

である。ところが

なので矛盾である。したがって、I n , J n , K n , L n のうち少なくとも1つは、無限に多くのゼロでない項を持つ。それを M n とおく。
さて

が有理数で

も有理数だと仮定する。すると、qb 2n + 1 Mn は整数で、n → ∞ のとき限りなく小さくなる。したがって十分大きな n に対して、qb 2n + 1 Mn = 0 となり、Mn = 0 となる。これは矛盾である。ゆえに、ニーベン・インケリの定理が証明された。
G.H.Hardy と E.M.Wright の証明
正の整数をnとし、cmを整数とするとき

とする。0<x<1において

となる。…(1)
πが有理数であると仮定し、 (a,bは正の整数)とする。
(a,bは正の整数)とする。

とする。 m<nまたは2n<mのとき

である。 n≦m≦2nのとき

なので、整数である。 それゆえ、任意のmに対して  は整数である。 したがって G(0) は整数である。
は整数である。 したがって G(0) は整数である。
f(x)=f(1-x)なので両辺を微分することにより



である。一般に

のとき

 .
.
すなわち

である。 よって

なので

G(0)=G(1)なのでG(1)も整数である。また

となる。さらに

となり、これは整数である。(1)より十分にnが大きいとき

となる。 これは矛盾である。
ランベルトによる証明
有理数 x に対する値 y = tan x が 0 または無理数であることから、その対偶を取れば、0 でない有理数 y に対する値 x = arctan y は無理数であることがわかる。よって、π = 4 arctan 1 は無理数である[7]。
より進んだ結果と未解決問題
ルジャンドルは π2 が無理数であることを示したが、現在では π の累乗は全て無理数であることが知られている(実は円周率は超越数であり,(非零有理数をべき指数とする)超越数のべき乗も超越数になるので(非零有理数をべき指数とする)円周率のべき乗は超越数になる。そうして超越数は無理数である)。実際、ドイツのフェルディナント・フォン・リンデマンは、1882年に π が超越数であることを示した。これは、さらに一般的なリンデマンの定理[8]の特別な場合である。この定理は、円周率のみならず、ネイピア数 e, 2の自然対数 log 2, 1 の正弦 sin 1 などが超越数であることを導く、非常に強力なものである。また、ユーリイ・ネステレンコ(英語版)は π と eπ が Q 上代数的独立であることを示した[9]。この事実は、π が無理数であることや超越数であることを内包している。
これらの進んだ結果が知られているにもかかわらず、円周率の性質が十分判明したとはいえない。例えば、その(任意の記数法において)小数展開の数字列が十分に「乱数的」であるといえるか(「真の乱数」による乱数列と、何か異なった性質がありはしないか)、例えば正規数であるか、という問題は(そうであろうとは一般に信じられてはいるが)いまだに未解決である。また、ππ や π + e のような単純な定数についても、無理数であるかどうかも分かっていないようなものがある。
脚注
[脚注の使い方]
- ^ 小平邦彦は、晩年のエッセイの中で「最近初めて証明を読んだ」と記している(小平 p. 79)。『数学セミナー』2004年12月号の特集「知っているようで知らない証明に再挑戦」で「π の超越性」が取り上げられた。
- ^ 歴史については Beckmann 16章 を参照。証明については Hairer & Wanner 1.6節 を参照。ランベルトの原論文は Mémoires sur quelques propriétés remarquables des quantités transcendantes, circulaires et logarithmiques. Mémoires de l'Académie royale des sciences de Berlin, année 1761/1768, 265-322 pdf ファイル
- ^ Ivan Niven, A simple proof that π is irrational, Bulletin of the American Mathematical Society, 53 (1947), 509. 論文の PDF ファイル
- ^ Jeffreys p.268
- ^ Aigner & Ziegler 6章。原論文は Y. Iwamoto, A proof that π2 is irrational, Journal of the Osaka Institute of Science and Technology 1 (1949), 147-148.
- ^ 初等教育においては、円周率の定義は「円周長の直径に対する比率」と学ぶ。この定義は初学者には受け入れ易いものの、現代数学の観点からは、曲線の長さの定義に依存しているという問題がある。そのため、現代数学においては、別の定義が採用されることが多い。円周率#定義も参照のこと。どの定義も結果的に同じ定数を定めることが従う。
- ^ a b c d L. Zhou and L. Markov, Recurrent Proofs of the Irrationality of Certain Trigonometric Values, arXiv:0911.1933.
- ^ 1885年にカール・ワイエルシュトラスが証明を簡潔にしたので、リンデマン–ワイエルシュトラスの定理とも呼ばれる。Beckmann 16章 を参照。定理の主張と証明については 塩川 2.7節 を参照。
- ^ 塩川 p. 93.
参考文献
- M. Aigner and G. M. Ziegler, Proofs from the Book, 3rd edition, Springer, 2003. ISBN 3540404600
- 蟹江幸博訳『天書の証明』シュプリンガー・フェアラーク東京、2002年(2nd edition の訳)ISBN 443170986X
- P. Beckmann, History of Pi, 3rd edition, St. Martin's Press, 1971 ISBN 0312381859
- 田尾陽一・清水韶光訳『π の歴史』筑摩書房、2006年 ISBN 4480089853
- E. Hairer and G. Wanner, Analysis by Its History, Undergraduate Texts in Mathematics, Springer-Verlag, 1996 ISBN 0387945512
- 蟹江幸博訳『解析教程』シュプリンガー東京、2006年(上巻)ISBN 4431712135(下巻)ISBN 4431712143
- H. Jeffreys, Scientific Inference, 3rd edition, Cambridge University Press, 1973 ISBN 0521084466
- 小平邦彦編『数学の学び方』岩波書店、1987年 ISBN 4000055119
- 塩川宇賢『無理数と超越数』森北出版、1999年3月30日。ISBN 4-627-06091-2。http://www.morikita.co.jp/shoshi/ISBN978-4-627-06091-3.html。 - 20~21頁に円周率の無理性の証明が掲載されている。
関連項目
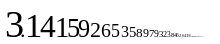
















![{\displaystyle \int _{0}^{\pi }f_{n}(x)\sin x\,dx={\bigg [}F'_{n}(x)\sin x-F_{n}(x)\cos x{\bigg ]}_{0}^{\pi }=F_{n}(\pi )+F_{n}(0)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25ac72a5cd8c10484999e764e3e33690e5f6ce81)











































