not to be confused with fungus

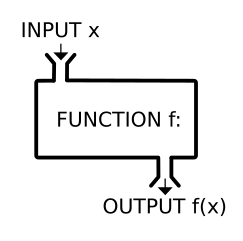
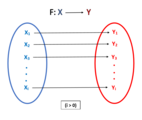
Fungsi merupakan suatu hubungan banyak ke satuatausatu ke satuantara unsur set ${\displaystyle X}$ yangdipanggil sebagai domain kepadaunsur set ${\displaystyle Y}$ yang dipanggil sebagai kodomain. Setiap unsur dalamset ${\displaystyle X}$ dipanggil sebagai'objek'atau'input'manakala setiap unsur di dalam set ${\displaystyle Y}$ dipanggil sebagai'imej'atau 'output'.

Terdapat dua notasi bagi menulis suatu hubungan fungsi ${\displaystyle f}$ dimana input ${\displaystyle x}$ dipetakan kepada output ${\displaystyle y}$, iaitu:

${\displaystyle f(x)=y}$ atau ${\displaystyle f:x\mapsto y}$

Sebagai contoh, suatu hubungan fungsi ${\displaystyle g}$ dimana setiap input ${\displaystyle x}$ akan menghasil output ${\displaystyle 2x+1}$ boleh ditulis seperti ini:

${\displaystyle g(x)=2x+1}$ atau ${\displaystyle g:x\mapsto 2x+1}$

Apabila kita inputkan suatu nilai kedalam suatu fungsi, kita hanya mesti gantikan semua pemboleh ubah dengan nilai itu. Contoh:

Katakan kita mempunyai suatu fungsi ${\displaystyle h}$, dimana ${\displaystyle h(z)=z^{2}+1}$. Untuk mencari nilai ${\displaystyle h(3)}$, kita hanya mesti gantikan semua pemboleh ubah ${\displaystyle z}$ dengan ${\displaystyle 3}$. Jadi;

${\displaystyle h(z)=z^{2}+1}$

${\displaystyle h(3)=(3)^{2}+1}$, gantikan semua pemboleh ubah ${\displaystyle z}$ dengan ${\displaystyle 3}$

${\displaystyle h(3)=9+1}$

${\displaystyle h(3)=10}$

Maka, ${\displaystyle h(3)=10}$

Walaupun nama fungsi selalunya dilabel dengan huruf abjad Rumi, fungsi kebanyakannya juga dilabelkan dengan huruf abjad Yunani atau suatu perkataan, contohnya:

> ${\displaystyle \zeta (s)}$, Fungsi Riemann-Zeta^[1]

> ${\displaystyle \pi (x)}$, Fungsi Kiraan Nombor Perdana^[2][3]

> ${\displaystyle \Gamma (z)}$, Fungsi Gamma^[4]

> ${\displaystyle Rayo(n)}$, Fungsi Rayo

> ${\displaystyle TREE(n)}$, Fungsi TREE

Catatan: Input hanya boleh dilabelkan dengan huruf abjad Rumi dan Yunani. ${\displaystyle x}$ adalah nama input yang paling popular untuk digunakan sebagai nama input serta dengan ${\displaystyle n}$ digunakan sebagai nama input apabila suatu fungsi hanya terima input nombor bulat dan ${\displaystyle z}$ selalunya digunakan apabila suatu fungsi boleh menerima nombor kompleks. Namun begitu, ia juga penting untuk diperhatikan bahawa pengarang dan ahli matematik mungkin lebih suka memilihi huruf yang berbeza dalam kerja mereka.

Domain adalah set bagi semua input yang boleh diterima oleh fungsi. Ia biasanya ditulis dalam notasi set dan notasi interval. Berikut adalah contoh asas:

Katakan suatu fungsi ${\displaystyle f}$ dimana ${\displaystyle f(x)={\frac {1}{x}}}$ . Domain bagi fungsi ini adalah ${\displaystyle (-\infty ,0)\cup (0,\infty )}$ atau ${\displaystyle \mathbb {R} \setminus \{0\}}$ kerana apabila ${\displaystyle 0}$ dimasukkan kedalam fungsi itu, ia menghasilkan ralat bahagian dengan 0. Maka, ${\displaystyle f(0)}$ adalah undefined dan ${\displaystyle 0}$ tidak disertakan dalam domainnya

Ini adalah satu lagi contoh asas:

Katakan suatu fungsi ${\displaystyle A}$ dimana ${\displaystyle A(k)=0^{k}}$. Domain bagi fungsi ini boleh ditulis sebagai ${\displaystyle (0,\infty )}$, ${\displaystyle \{k:k>0\}}$ atau ${\displaystyle \mathbb {R} ^{+}}$. Ia sebab apabila kita inputkan suatu nombor negatif ke dalam fungsi itu, ia menghasikan ralat bahagi ${\displaystyle 0}$. Maka, ${\displaystyle A(n)}$ dimana ${\displaystyle n\in \mathbb {R^{-}} }$ adalah undefined dan semua nombor dalam set ${\displaystyle \mathbb {R} ^{-}}$ tidak disertai ke dalam domainnya.

Kodomain adalah set bagi semua nilai yang wujud manakala julat adalah set bagi semua output yang hanya boleh dikeluari oleh suatu fungsi. Ia biasanya ditulis dalam notasi set dan notasi interval.

Fungsi mempunyai 3 kelas fungsi iaitu fungsi injektif, surjektif dan bijektif.

Fungsi injektif (juga dipanggil sebagai injeksi atau satu-ke-satu) merupakan suatu hubungan fungsi dimana semua inputnya dipetakan kepada suatu output tetapi kodomain masih ada nilai yang mustahil untuk dipetakan dari fungsi tersebut.

Sebagai contoh,

Katakan suatu fungsi ${\displaystyle B}$ dimana ${\displaystyle B(x)=x^{2}}$ dan kodomainnya adalah semua nilai dalam ${\displaystyle \mathbb {R} }$. Fungsi ${\displaystyle B}$ adalah suatu fungsi injektif kerana terdapat nilai dalam kodomainnya yang tidak dipetakan oleh inputnya {BELUM SIAP}

Fungsi surjektif (juga dipanggil sebagai surjeksi) merupakan suatu hubungan fungsi dimana setiap inputnya dipetakan kepada suatu output tetapi lebih dari satu input mungkin mempunyai suatu output-output yang sama.

Fungsi bijektif (juga dipanggil sebagai bijeksi) merupakan suatu gabungan definisi hubungan fungsi injektif dan surjektif dimana setiap input hanya mempuyai satu output sendirinya dan tidak mempunyai output yang berkongsian dengan input lain.

• 
  Hubungan Fungsi Injektif
• 
  Hubungan Fungsi Surjektif
• 
  Hubungan Fungsi Bijektif

• Wolfram Mathworld