Johnson-graaf

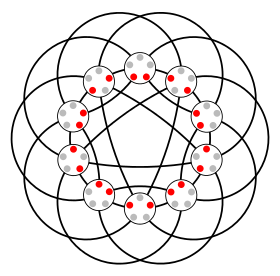
Een Johnson-graaf ${\displaystyle J(n,k)}$ is een ongerichte graaf met als knopen alle deelverzamelingen met ${\displaystyle k}$ elementen uit een verzameling van ${\displaystyle n}$ elementen. Twee knopen zijn door een kant verbonden als en alleen als hun corresponderende deelverzamelingen exact ${\displaystyle k-1}$ gemeenschappelijke elementen hebben.

Johnson-grafen zijn genoemd naar de Amerikaanse wiskundige Selmer M. Johnson. Ze staan in verband met de zogenaamde Johnson-schema's, een klasse van associatieschema's in de algebraïsche combinatoriek. Ze hebben een hoge mate van symmetrie.

• ${\displaystyle J(n,1)}$ is isomorf met de volledige graaf ${\displaystyle K_{n}}$
• ${\displaystyle J(n,0)}$ is een triviale graaf bestaande uit een enkele knoop, corresponderend met de lege verzameling.
• ${\displaystyle J(n,n)}$ is een triviale graaf bestaande uit een enkele knoop, corresponderend met de volledige verzameling van ${\displaystyle n}$ elementen.
• ${\displaystyle J(5,2)}$ is de complementgraaf van de Petersen-graaf. Algemeen geldt dat ${\displaystyle J(n,2)}$ de complementgraaf is van de Kneser-graaf ${\displaystyle K(n,2)}$.

Merk op dat ${\displaystyle J(n,k)}$ en ${\displaystyle J(n,n-k)}$ isomorf zijn. De ene graaf kan uit de andere afgeleid worden door elke deelverzameling van ${\displaystyle k}$ elementen af te beelden op haar complement.

De Johnson-graaf ${\displaystyle J(n,k)}$ heeft ${\displaystyle {\binom {n}{k}}}$ knopen en ${\displaystyle {\frac {k(n-k)}{2}}{\binom {n}{k}}}$ kanten.

Johnson-grafen zijn reguliere grafen; alle knopen hebben dezelfde graad. Ze zijn bovendien afstandsregulier.

De afstand tussen twee knopen (dit is de lengte van het kortste pad ertussen) in een Johnson-graaf is gelijk aan de helft van de Hammingafstand tussen hun corresponderende deelverzamelingen. Bijvoorbeeld de deelverzamelingen {1,2} en {3,4} van {1,2,3,4,5} kan men voorstellen door de "woorden" 11000 en 00110. De Hammingafstand daartussen is 4, terwijl de afstand in de Johnson-graaf ${\displaystyle J(5,2)}$ tussen de twee deelverzamelingen gelijk is aan 2.

Brian Alspach bewees in 2013 dat elke Johnson-graaf ${\displaystyle J(n,k)}$ Hamilton-verbonden is voor alle ${\displaystyle n>1}$. Dit betekent dat er een Hamiltonpad bestaat tussen elk paar knopen.^[1]

De Johnson-graaf ${\displaystyle J(n,k)}$ is nauw verwant met het Johnson-schema met ${\displaystyle k}$ klassen, dat ook wordt aangeduid als ${\displaystyle J(n,k)}$. Dit is een associatieschema gedefinieerd op de deelverzamelingen met ${\displaystyle k}$ elementen van een verzameling met ${\displaystyle n}$ elementen.

Twee deelverzamelingen behoren tot relatie ${\displaystyle R_{i}}$ (of zijn geassocieerd met het getal ${\displaystyle i}$) indien ze exact ${\displaystyle k-i}$ elementen gemeenschappelijk hebben. De Johnson-graaf is de voorstelling van de relatie ${\displaystyle R_{1}}$.