Regula falsi

Regula falsi (łac. fałszywa linia prosta, fałszywa reguła) – algorytm rozwiązywania równań nieliniowych jednej zmiennej.

Na funkcję ${\displaystyle y=f(x)}$ nakładane są następujące ograniczenia:

1. W przedziale [a,b] znajduje się dokładnie jeden pojedynczy pierwiastek.
2. Na końcach przedziału funkcja ma różne znaki: ${\displaystyle f(a)f(b)<0.}$
3. Pierwsza i druga pochodna istnieją i mają na tym przedziale stałe znaki.

Algorytm przebiega następująco:

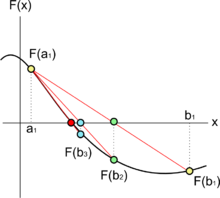
• Na początku przez punkty ${\displaystyle A=(a,f(a))}$ i ${\displaystyle B=(b,f(b))}$ przeprowadzana jest cięciwa.
• Punkt przecięcia ${\displaystyle x_{1}}$ z osią OX jest brany jako pierwsze przybliżenie pierwiastka.
• Jeśli to przybliżenie jest wystarczająco dobre, algorytm kończy się.
• Jeśli nie, to prowadzona jest cięciwa przez punkty ${\displaystyle (x_{1},f(x_{1}))}$ oraz ${\displaystyle A}$ lub ${\displaystyle B}$ – wybierany jest ten punkt, którego rzędna ma znak przeciwny do ${\displaystyle f(x_{1}).}$ Jednak w praktyce, dzięki ograniczeniu nr 3 już na początku algorytmu wiadomo, który z tych punktów będzie stały, tzn. wybierany za każdym razem.
• Następnie wyznaczane jest przecięcie nowo wyznaczonej cięciwy z osią OX ${\displaystyle (x_{i})}$ i algorytm powtarza się.

Nazwa metody pochodzi od łacińskich słów: regula^[1] znaczące zarówno linię prostą, jak i regułę i falsus, fałszywy – metoda bazuje na fałszywym twierdzeniu (regule), że na pewnym przedziale funkcja jest liniowa. Można więc tę nazwę przetłumaczyć zarówno jako „fałszywa linia prosta”, jak i „fałszywa reguła” i obydwa te tłumaczenia mają w tym kontekście sens.

${\displaystyle x_{1}={\frac {af(b)-bf(a)}{f(b)-f(a)}}}$

${\displaystyle x_{i+1}=\left\{{\begin{matrix}{\frac {x_{i}f(a)-af(x_{i})}{f(a)-f(x_{i})}}&gdy&f(a)f(x_{i})<0\\[.5em]{\frac {x_{i}f(b)-bf(x_{i})}{f(b)-f(x_{i})}}&gdy&f(b)f(x_{i})<0\end{matrix}}\right.}$

dla ${\displaystyle i=1,2,...}$

Inne numeryczne metody wyznaczania pierwiastków równania nieliniowego:

• algorytm Illinois (zmodyfikowana metoda siecznych)
• metoda bisekcji
• metoda Newtona (metoda stycznych)
• metoda siecznych
• odwrotna interpolacja kwadratowa

• [1]