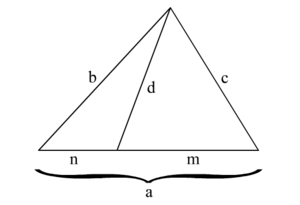
Twierdzenie Stewarta

Twierdzenie Stewarta – twierdzenie planimetrii wykorzystywane do obliczania długości czewian. Zostało udowodnione i opublikowane przez szkockiego matematyka Matthew Stewarta w 1746 roku.

Niech ${\displaystyle a,}$ ${\displaystyle b,}$ i ${\displaystyle c}$ będą długościami boków trójkąta. Niech ${\displaystyle d}$ będzie długością odcinka łączącego pewien punkt leżący na boku długości ${\displaystyle a}$ z wierzchołkiem naprzeciw tego boku (odcinek taki nazywamy czewianą). Jeżeli poprowadzony odcinek dzieli bok długości ${\displaystyle a}$ na odcinki o długościach ${\displaystyle m}$ i ${\displaystyle n}$ sąsiadujące odpowiednio z bokami ${\displaystyle c}$ i ${\displaystyle b}$, to:

${\displaystyle b^{2}m+c^{2}n=a(d^{2}+mn).}$^[1]

Niech ${\displaystyle \theta }$ będzie kątem między ${\displaystyle m}$ i ${\displaystyle d,}$ zaś ${\displaystyle \theta '}$ kątem między ${\displaystyle n}$ i ${\displaystyle d.}$ Stosując twierdzenie cosinusów dla kątów ${\displaystyle \theta }$ oraz ${\displaystyle \theta '}$, otrzymujemy równości

${\displaystyle c^{2}=m^{2}+d^{2}-2dm\cos \theta ,}$

(1)

${\displaystyle b^{2}=n^{2}+d^{2}-2dn\cos \theta '.}$

(2)

Ponieważ kąty ${\displaystyle \theta }$ i ${\displaystyle \theta '}$są przyległe, zachodzi równość ${\displaystyle \cos \theta '=-\cos \theta ,}$ czyli

${\displaystyle b^{2}=n^{2}+d^{2}+2dn\cos \theta }$

(3)

Mnożąc równanie (1) przez ${\displaystyle n,}$ a równanie (3) przez ${\displaystyle m}$ i dodając je stronami, otrzymujemy

${\displaystyle {\begin{aligned}b^{2}m+c^{2}n&=nm^{2}+n^{2}m+(m+n)d^{2}\\&=(m+n)(mn+d^{2})\\&=a(mn+d^{2}).\end{aligned}}}$