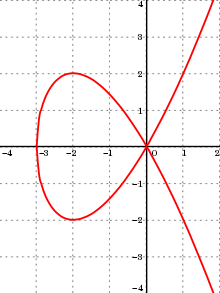Tschirnhausen立方曲線 y 2 = x 3 + 3 x 2 . {\displaystyle y^{2}=x^{3}+3x^{2}.} Talbot曲线 也稱為切恩豪斯立方曲線 ,為一平面曲線 ,極坐標 方程式如下
r = a sec 3 ( θ / 3 ) . {\displaystyle r=a\sec ^{3}(\theta /3).}
埃伦弗里德·瓦尔特·冯·切恩豪斯 、紀堯姆·德·洛必達 及歐仁·查爾斯·加泰羅尼亞 都曾研究此曲線。在R C Archibald於1900年發表的論文中將此稱為切恩豪斯立方曲線,不過也稱為洛必達立方曲線(de L'Hôpital's cubic)或加泰羅尼亞三等分角线(trisectrix of Catalan)。
令 t = tan ( θ / 3 ) {\displaystyle t=\tan(\theta /3)} 棣莫弗公式 可得
x = a cos θ sec 3 θ 3 = a ( cos 3 θ 3 − 3 cos θ 3 sin 2 θ 3 ) sec 3 θ 3 {\displaystyle x=a\cos \theta \sec ^{3}{\frac {\theta }{3}}=a(\cos ^{3}{\frac {\theta }{3}}-3\cos {\frac {\theta }{3}}\sin ^{2}{\frac {\theta }{3}})\sec ^{3}{\frac {\theta }{3}}} = a ( 1 − 3 tan 2 θ 3 ) = a ( 1 − 3 t 2 ) {\displaystyle =a\left(1-3\tan ^{2}{\frac {\theta }{3}}\right)=a(1-3t^{2})} y = a sin θ sec 3 θ 3 = a ( 3 cos 2 θ 3 sin θ 3 − sin 3 θ 3 ) sec 3 θ 3 {\displaystyle y=a\sin \theta \sec ^{3}{\frac {\theta }{3}}=a\left(3\cos ^{2}{\frac {\theta }{3}}\sin {\frac {\theta }{3}}-\sin ^{3}{\frac {\theta }{3}}\right)\sec ^{3}{\frac {\theta }{3}}} = a ( 3 tan θ 3 − tan 3 θ 3 ) = a t ( 3 − t 2 ) {\displaystyle =a\left(3\tan {\frac {\theta }{3}}-\tan ^{3}{\frac {\theta }{3}}\right)=at(3-t^{2})} 可以得到此曲線的參數式 。參數t可以消去,得到以下方程式
27 a y 2 = ( a − x ) ( 8 a + x ) 2 {\displaystyle 27ay^{2}=(a-x)(8a+x)^{2}} 若此參數式水平平移8a ,方程式會變成
x = 3 a ( 3 − t 2 ) {\displaystyle x=3a(3-t^{2})} y = a t ( 3 − t 2 ) {\displaystyle y=at(3-t^{2})} 或
x 3 = 9 a ( x 2 − 3 y 2 ) {\displaystyle x^{3}=9a\left(x^{2}-3y^{2}\right)} 因此可以得到另一個極坐標方程式
r = 9 a ( sec θ − 3 sec θ tan 2 θ ) {\displaystyle r=9a\left(\sec \theta -3\sec \theta \tan ^{2}\theta \right)}
J. D. Lawrence, A Catalog of Special Plane Curves . New York: Dover, 1972, pp. 87-90.
埃里克·韦斯坦因 . Tschirnhausen Cubic. MathWorld. "Tschirnhaus' Cubic" at MacTutor History of Mathematics Archive(页面存档备份,存于互联网档案馆 ) "Cubique de Tschirnhausen" at Encyclopédie des Formes Mathématiques Remarquables(页面存档备份,存于互联网档案馆 ) (in French)
这是一篇關於幾何學 的小作品。您可以通过编辑或修订扩充其内容。