パップスの六角形定理

パップスの定理またはパップスの六角形定理（パップスのろっかくけいていり、英: Pappus's hexagon theorem）とはアレキサンドリアのパップスの名を冠する定理の一つである^[1]。

• ${\displaystyle A,B,C}$と${\displaystyle a,b,c}$がそれぞれ共線であるとき、${\displaystyle Ab}$と${\displaystyle aB}$の交点を${\displaystyle X}$, ${\displaystyle Ac}$と${\displaystyle aC}$の交点を${\displaystyle Y}$、${\displaystyle Bc}$と${\displaystyle bC}$の交点${\displaystyle Z}$として、${\displaystyle X,Y,Z}$は共線である。またこの線をパップス線（Pappus line）という。また${\displaystyle X,Y,Z}$は六角形${\displaystyle AbCaBc}$の3本の主対角線^[2]の交点である。

この定理は任意の射影平面上で成立するが、非可換体上では成立しない^[3]。パップスの定理の成り立つ射影平面はパップス平面（pappian planes）と呼ばれる。

先述の六角形${\displaystyle AbCaBc}$について、${\displaystyle Ab\parallel aB,Bc\parallel bC}$ならば（パップス線${\displaystyle u}$は無限遠直線となって）2番目の図の様に、アフィン幾何学におけるパップスの定理を得る。

パップス線${\displaystyle u}$と直線${\displaystyle g,h}$が共点ならば、little version of Pappus's theoremを得る^[3][4]。

交点定理（英語版）によれば、共点な直線${\displaystyle A,B,C}$と、${\displaystyle A,B,C}$とは異なる点で共点な直線${\displaystyle a,b,c}$において、直線の交点${\displaystyle A\cap b}$と${\displaystyle a\cap B}$を結ぶ直線を${\displaystyle x}$、${\displaystyle A\cap c}$と${\displaystyle a\cap C}$を結ぶ直線を${\displaystyle y}$、${\displaystyle B\cap c}$と${\displaystyle b\cap C}$を結ぶ直線を${\displaystyle z}$とすれば、${\displaystyle x,y,z}$は共点である（${\displaystyle \cap }$で2直線の交点を示す）。

パップスの定理はパスカルの定理の特別な場合である。パスカルの定理に出現する円錐曲線を2直線に退化させれば、パップスの定理を得る。パスカルの定理はまた、ケイリー＝バッハラッハの定理の特別な場合である。

パップス配置（英語版）はパップスの定理に出現する9つの点と直線の配置（英語版）である。一般には、パップス線は直線${\displaystyle ABC}$と${\displaystyle abc}$の交点を通らない^[5]。 この配置は自己双対性を持つ。したがって直線${\displaystyle Bc,bC,XY}$は${\displaystyle x,y,z}$のような双対の性質を持ち、${\displaystyle X,Y,Z}$の共線は${\displaystyle Bc,bC,XY}$の共点と対応する。パップス配置のレヴィグラフ（英語版）はパップスグラフ（英語版）と呼ばれる。パップスグラフは18個の頂点と27個の辺を持つ2部の距離正則（英語版）なグラフである。

アフィン形式で、ある座標設定でのパップスの定理が証明されれば、それを適当に射影することで、一般のパップスの定理を証明できる。

アフィン平面（英語版）では${\displaystyle g\not \parallel h}$と${\displaystyle g\parallel h}$を区別する必要がある。また、単純な証明のためには、座標設定を巧く行わなければならない。

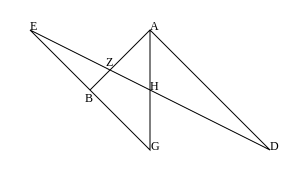
場合1: ${\displaystyle g,h}$ が点${\displaystyle S=g\cap h}$で交わる場合。図の様に座標を設定する。

${\displaystyle \;S=(0,0),\;A=(0,1),\;c=(1,0)\;}$

${\displaystyle \;B=(0,\gamma ),\;C=(0,\delta ),\;\gamma ,\delta \notin \{0,1\}}$

${\displaystyle Bc,\;Cb}$の平行より${\displaystyle b=({\tfrac {\delta }{\gamma }},0)}$を、${\displaystyle Ab,Ba}$の平行より${\displaystyle a=(\delta ,0)}$を得る。故に、${\displaystyle Ca}$は傾き${\displaystyle -1}$であるから、${\displaystyle Ac}$と平行である。

場合2: ${\displaystyle g\parallel h\ }$ である場合(小定理)。次の様に座標を設定する。

${\displaystyle \;c=(0,0),\;b=(1,0),\;A=(0,1),\;B=(\gamma ,1),\;\gamma \neq 0}$.

${\displaystyle Ab\parallel Ba}$と${\displaystyle cB\parallel bC}$から、${\displaystyle \;C=(\gamma +1,1)\;}$と${\displaystyle \;a=(\gamma +1,0)\;}$を得て、${\displaystyle \;Ac\parallel Ca\;}$が証明される。

同次座標（英語版）系で、点の座標を次のように設定する。

${\displaystyle C=(1,0,0),\;c=(0,1,0),\;X=(0,0,1),\;A=(1,1,1)}$.

直線${\displaystyle AC,Ac,AX}$の方程式をそれぞれ ${\displaystyle x_{2}=x_{3},\;x_{1}=x_{3},\;x_{2}=x_{1}}$とすれば、点${\displaystyle B,Y,b}$ はある${\displaystyle p,q,r}$を用いて

${\displaystyle B=(p,1,1),\;Y=(1,q,1),\;b=(1,1,r)}$

と書ける。直線${\displaystyle XB,CY,cb}$の方程式はそれぞれ${\displaystyle x_{1}=x_{2}p,\;x_{2}=x_{3}q,\;x_{3}=x_{1}r}$となる。したがってこの3直線が一点${\displaystyle a}$で交わることは${\displaystyle rqp=1}$と同値である。

直線${\displaystyle Cb,cB,XY}$の方程式はそれぞれ${\displaystyle x_{2}=x_{1}q,\;x_{1}=x_{3}p,\;x_{3}=x_{2}r}$となり、一点${\displaystyle Z}$で交わる条件は${\displaystyle rpq=1}$である。可換であるから${\displaystyle pq=qp}$。故に${\displaystyle Cb,cB,XY}$の共点の条件は他の8本の線が共点であることとなる。これは、${\displaystyle X,Y,Z}$ の共線と同値である。

この証明によって、パップスの定理の成立には可換性が必要であることが分かる^[6]。ドイツの数学者、ゲルハルト・ヘッセンベルク（英語版）はデザルグの定理を含んでいることを示した^[7][8][6]。一般に、射影平面において、パップスの定理の成立と可換体であることは同値である。パップスの定理を含まない射影平面は非可換なデザルグ射影平面で、非デザルグ平面（英語版） である。

同次座標による証明は${\displaystyle C,c,X}$の共線は起こらないことを条件としている。${\displaystyle C,c,X}$が共線である場合は別の証明を用いる必要がある。

射影幾何学の双対性（英語版）よりパップスの定理の双対も成り立つ。

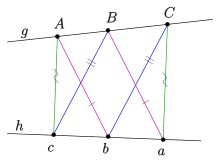
6本の直線${\displaystyle A,b,C,a,B,c}$が${\displaystyle G,H}$を中心とする束を成すように選ぶ。

${\displaystyle X:=(A\cap b)(a\cap B),}$

${\displaystyle Y:=(c\cap A)(C\cap a),}$

${\displaystyle Z:=(b\cap C)(B\cap c)}$

は点${\displaystyle U}$で共点である。左の図は射影幾何学、右の図はアフィン幾何学による表現である。アフィン幾何学の方では${\displaystyle G,H}$は無限遠点である。${\displaystyle U}$が${\displaystyle GH}$上にあれば、パップスの定理の"dual little theorem"を得る。

• 
• 

アフィン形式のlittle theoremので得る点${\displaystyle U}$が${\displaystyle GH}$上にある、つまり無限遠点である場合、トムセンの定理を得る。トムセンの図形は射影平面の公理の決定に大きな役割を果たす^[9]。トムソンの図形の閉形の証明は"little theorem"の証明により行われる。しかし、次のように、より簡単で直接的な証明も存在する。トムセンの定理の主張には接続、交差、平行のみが用いられるためにアフィン写像によって不変である。三角形の頂点の座標を${\displaystyle P=(0,0),\;Q=(1,0),\;R=(0,1)}$と置く。また最初の点を${\displaystyle (0,\lambda )}$ とする。6回の操作を経て最後の点が${\displaystyle (0,\lambda )}$に戻ることを証明すればよい。

• 
  トムセンの図形（三角形${\displaystyle PQR}$と点${\displaystyle \color {red}1,2,3,4,5,6}$) 。
• 
  証明に用いる図

パップスの定理とその双対の他の特徴づけに次の主張がある。

• 六角形の6つの頂点が3点ずつ2本の直線上にあるとき、六角形の主対角線の交点は共線である^[10]。
• 9つの点を行列に書き直して、パーマネントとして評価する。1,2行目と、その6つの"対角"が共線ならば3行目も共線である。

${\displaystyle \left|{\begin{matrix}A&B&C\\a&b&c\\X&Y&Z\end{matrix}}\right|}$

つまり直線${\displaystyle \ ABC,abc,AbZ,BcX,CaY,XbC,YcA,ZaB\ }$があったとき、パップスの定理は直線${\displaystyle XYZ}$の存在を主張している。行列に双対の形式を当てはめると、${\displaystyle (A,B,C)}$などは共点な直線となる^[11]。

• 2つの直線上にそれぞれ3つの異なる点があるとする。一方の直線上の点ともう一方の直線上の点を1対1に対応させる。このとき、対応していない点を結ぶ直線はある直線上で交わる^[12]。
• 2つの三角形が2通りの対応で配景であるとき、3つ目の対応でも配景である^[7]。${\displaystyle AB,CD,EF}$が共点で且つ${\displaystyle DE,FA,BC}$が共点ならば、${\displaystyle AD,BE,CF}$も共点である^[11]。

これらの性質の最も早い形はパップスの著書のVIIの性質138,139,141,143で知られていた^[13]。また、これらの性質はエウクレイデスのPorismsの巻VIIの一部にある補題XII,XIII,XV,XVIIである。

エウクレイデスの書にある補題は今日では複比として知られる概念を用いて証明されている。また、先の3つの補題も利用されている。一つ目は補題IIIである。 (パップスの記述とは、GとΓ、DとΔ、JとΘ、LとΛが対応している)。

3つの共点線AB,AG,ADがあって、JB,JEがJで交わっている。またKLはAZと平行である。このとき

KJ : JL :: (KJ : AG & AG : JL) :: (JD : GD & BG : JB).

である。これらは今日、等式として次の様に表される^[14]。

KJ/JL = (KJ/AG)(AG/JL) = (JD/GD)(BG/JB).

最右辺 ( JD : GD と BG : JBの積) は、共線点J, G, D, Bに対して複比として知られるもので、(J, G; D, B)とも書かれる。つまりAで交わる3線のうち、JDの取り方は複比と無関係であることが示された。

(J, G; D, B) = (J, Z; H, E).

直線JEがAを通るどの辺（直線）にあたるかは重要ではない。特に図を変えれば、以下の様になることもある（補題X） 。

先述のように(J, G; D, B) = (J, Z; H, E)である。パップスはこれを証明しなかったが、 補題Xはこの構図の逆「2つの複比が等しく図の様にBE,DHがAで交わるとすれば、点G,A,Zは共線である」を表している。

JK,AGが交わらない場合は複比を (J, ∞; K, L) = (J, G; D, B)の様に書くことができる。パップスはこれを補題XIで示している。

当時の記法ではDE.ZH : EZ.HD :: GB : BEとなるが、これは

(D, Z; E, H) = (∞, B; E, G).

という表現に等しい。

次の図は補題XIIである。

この図は補題XIIIと意味する所は同じだがBA,DGが辺の延長にある点Nで交わっている。どのような場合でも、Gを通る直線がAを通る直線と交わっているとすれば (そして複比の不変性を利用すれば）、補題IIIとXIを次のように得る。

(G, J; E, H) = (G, D; ∞ Z).

Dを通る直線がBを通る直線と交わっているとすれば、

(L, D; E, K) = (G, D; ∞ Z).

を得る。したがって(E, H; J, G) = (E, K; D, L)である。また補題Xより、H,M,Kは共線である。これは、六角形ADEGBZの主対角線の交点の共線を表している。

補題XVとXVIIは、直線HK,BGの交点をMとして、A,M,Gの共線を示している。これは六角形BEKHZGの主対角線の交点の共線を示している。

• メネラウスの定理
• デザルグの定理
• ブリアンションの定理

1. ^ 細川藤右衛門『射影幾何学』岩波書店、1943年、89頁。doi:10.11501/1063403。 
2. ^ 『近世幾何学 (帝国百科全書 ; 第179編)』藤田外次郎、1908年、150頁。doi:10.11501/828609。 
3. ^ ^{a b} Coxeter 1969, pp. 236–7
4. ^ Rolf Lingenberg: Grundlagen der Geometrie, BI-Taschenbuch, 1969, p. 93
5. ^ ただし、${\displaystyle ABC}$と${\displaystyle abc}$で配景が起こる、つまり${\displaystyle Aa,Bb,Cc}$が共点ならば、パップス線と${\displaystyle ABC}$と${\displaystyle abc}$も共点である。
6. ^ ^{a b} 窪田忠彦『幾何学の基礎 第3版 (岩波全書 ; 第104)』岩波書店、1946年、52-60,101-102,127頁。doi:10.11501/1211294。 
7. ^ ^{a b} Coxeter 1969, p. 238
8. ^ (Dembowski 1968, pg. 159, footnote 1)によれば, ヘッセンベルクHessenberg (1905)の元の証明は完全ではなかった。彼は デザルグ配置で起こるいくつかの問題を見逃した。完全な証明はCronheim 1953によって行われた。
9. ^ W. Blaschke: Projektive Geometrie, Springer-Verlag, 2013, ISBN 3034869320, S. 190
10. ^ Coxeter 1969, p. 231
11. ^ ^{a b} Coxeter 1969, p. 233
12. ^ Whicher 1971, chapter 14
13. ^ Heath (Vol. II, p. 421)はこれらの性質を引用している。後の2つは前の二つの逆として知られる。 Kline (p. 128)は性質139のみを引用している。性質の番号付けはHultschによる。
14. ^ 古代ギリシャでこのように記述された理由は、当時は比というものは、数論や幾何学の対象として見られていなかったことが挙げられる。また、現在の私たちの「等しい」と言う概念は幾何学的に比にも応用できるが、古代ギリシャ人は今日でいう合同として「等しい」という概念を扱っていた。このような意味で線分は等価ではなく、比は等しいとは考えなかった。

• CoxeterHarold Scott MacDonald『Introduction to Geometry』（2nd）John Wiley & Sons、New York、1969年。ISBN 978-0-471-50458-0。MR123930。 
• Cronheim, A. (1953), “A proof of Hessenberg's theorem”, Proceedings of the American Mathematical Society 4 (2): 219–221, doi:10.2307/2031794, JSTOR 2031794, https://jstor.org/stable/2031794 
• Dembowski, Peter (1968), Finite Geometries, Berlin: Springer-Verlag 
• Heath, Thomas (1981) [1921], A History of Greek Mathematics, New York: Dover Publications 
• Hessenberg, Gerhard (1905), “Beweis des Desarguesschen Satzes aus dem Pascalschen”, Mathematische Annalen (Berlin / Heidelberg: Springer) 61 (2): 161–172, doi:10.1007/BF01457558, ISSN 1432-1807 
• Hultsch, Fridericus (1877), Pappi Alexandrini Collectionis Quae Supersunt, Berlin 
• Kline, Morris (1972), Mathematical Thought From Ancient to Modern Times, New York: Oxford University Press 
• Pambuccian, Victor; Schacht, Celia (2019), “The axiomatic destiny of the theorems of Pappus and Desargues”, in Dani, S. G.; Papadopoulos, A., Geometry in history, Springer, pp. 355–399, ISBN 978-3-030-13611-6 
• WhicherOlive『Projective Geometry』Rudolph Steiner Press、1971年。ISBN 0-85440-245-4。 

• Pappus's hexagon theorem at cut-the-knot
• Dual to Pappus's hexagon theorem at cut-the-knot
• Pappus’s Theorem: Nine proofs and three variations
• “平面幾何の美しい定理4つ”. 高校数学の美しい物語. 2024年7月24日閲覧。