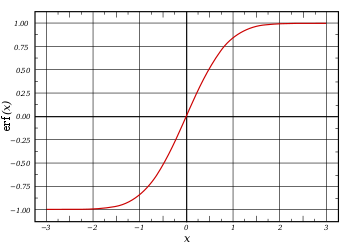
Wykres funkcji błędu Wykres funkcji błędu (2) Funkcja błędu Gaussa – funkcja nieelementarna, która występuje w rachunku prawdopodobieństwa , statystyce oraz w teorii równań różniczkowych cząstkowych. Jest zdefiniowana jako
erf ( x ) = 2 π ∫ 0 x e − t 2 d t . {\displaystyle \operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,\mathrm {d} t.} Funkcja erf {\displaystyle \operatorname {erf} } uzupełniającą funkcją błędu erfc : {\displaystyle \operatorname {erfc} {:}}
erfc ( x ) ≡ 1 − erf ( x ) = 2 π ∫ x ∞ e − t 2 d t . {\displaystyle {\begin{aligned}\operatorname {erfc} (x)&\equiv 1-\operatorname {erf} (x)\\&={\frac {2}{\sqrt {\pi }}}\int _{x}^{\infty }e^{-t^{2}}\,\mathrm {d} t.\end{aligned}}} Definiuje się także zespoloną funkcję błędu w ( x ) , {\displaystyle w(x),}
w ( x ) = e − x 2 erfc ( − i x ) . {\displaystyle w(x)=e^{-x^{2}}\operatorname {erfc} (-ix).}
Funkcja błędu jest nieparzysta :
erf ( z ) = − erf ( − z ) . {\displaystyle \operatorname {erf} (z)=-\operatorname {erf} (-z).} Ponadto należy zauważyć, że prawdziwe jest równanie:
erf ( z ∗ ) = ( erf ( z ) ) ∗ , {\displaystyle \operatorname {erf} (z^{*})=(\operatorname {erf} (z))^{*},} gdzie z ∗ {\displaystyle z^{*}} sprzężenie zespolone liczby z . {\displaystyle z.}
Dla osi rzeczywistej funkcja błędu przyjmuje następujące granice:
erf ( ± ∞ ) = ± 1 , {\displaystyle \operatorname {erf} (\pm \infty )=\pm 1,} natomiast dla osi urojonej:
erf ( ± i ∞ ) = ± i ∞ . {\displaystyle \operatorname {erf} (\pm i\infty )=\pm i\infty .} Funkcja błędu jest ściśle związana z rozkładem normalnym Gaussa . Można to zauważyć, wyliczając pochodną i funkcję pierwotną funkcji błędu:
d d z erf ( z ) = 2 π e − z 2 , {\displaystyle {\frac {d}{dz}}\operatorname {erf} (z)={\frac {2}{\sqrt {\pi }}}e^{-z^{2}},} F ( z ) = z erf ( z ) + e − z 2 π . {\displaystyle F(z)=z\,\operatorname {erf} (z)+{\frac {e^{-z^{2}}}{\sqrt {\pi }}}.}
Szereg Taylora Przez zapisanie prawej strony definicji jako szereg Taylora i całkowanie, można dowieść, że
erf ( x ) = 2 π ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) n ! = 2 π ( x − x 3 3 + x 5 10 − x 7 42 + x 9 216 − … ) {\displaystyle {\begin{aligned}\operatorname {erf} (x)&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)n!}}\\&={\frac {2}{\sqrt {\pi }}}\left(x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{10}}-{\frac {x^{7}}{42}}+{\frac {x^{9}}{216}}-\ \ldots \right)\end{aligned}}} dla każdego rzeczywistego x . {\displaystyle x.}
Dla | x | ≪ 1 , {\displaystyle |x|\ll 1,}
erf ( x ) = 2 π e − x 2 ∑ n = 0 ∞ 2 n ( 2 n + 1 ) ! ! x 2 n + 1 = 2 π e − x 2 ( x + 2 x 3 1 ⋅ 3 + 4 x 5 1 ⋅ 3 ⋅ 5 + 8 x 7 1 ⋅ 3 ⋅ 5 ⋅ 7 + … ) , {\displaystyle {\begin{aligned}\operatorname {erf} (x)&={\frac {2}{\sqrt {\pi }}}e^{-x^{2}}\sum _{n=0}^{\infty }{\frac {2^{n}}{(2n+1)!!}}x^{2n+1}\\&={\frac {2}{\sqrt {\pi }}}e^{-x^{2}}\left(x+{\frac {2x^{3}}{1\cdot 3}}+{\frac {4x^{5}}{1\cdot 3\cdot 5}}+{\frac {8x^{7}}{1\cdot 3\cdot 5\cdot 7}}+\ldots \right),\end{aligned}}} gdzie k ! ! {\displaystyle k!!} silnię podwójną liczby k . {\displaystyle k.}
Dla | x | ≫ 1 , {\displaystyle |x|\gg 1,}
erf ( x ) = 1 − e − x 2 π ∑ n = 0 ∞ ( − 1 ) n ( 2 n − 1 ) ! ! 2 n x − 2 n − 1 ) = 1 − e − x 2 π ( 1 x − 1 2 x 3 + 1 ⋅ 3 4 x 5 − 1 ⋅ 3 ⋅ 5 8 x 7 + … ) . {\displaystyle {\begin{aligned}\operatorname {erf} (x)&=1-{\frac {e^{-x^{2}}}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n-1)!!}{2^{n}}}x^{-2n-1)}\\&=1-{\frac {e^{-x^{2}}}{\sqrt {\pi }}}\left({\frac {1}{x}}-{\frac {1}{2x^{3}}}+{\frac {1\cdot 3}{4x^{5}}}-{\frac {1\cdot 3\cdot 5}{8x^{7}}}+\ldots \right).\end{aligned}}}
Jak można łatwo sprawdzić graficznie funkcje błędu można dobrze i zwięźle przybliżyć przez podobnie wyglądające i trochę zdeformowane funkcje cyklometryczne i funkcje hiperboliczne typu tangens, tzn. arctg ( x ) {\displaystyle \operatorname {arctg} (x)} tgh ( x ) : {\displaystyle \operatorname {tgh} (x){:}}
erf ( x ) ≈ 2 π arctg [ 2 x ( 1 + x 4 ) ] {\displaystyle \operatorname {erf} (x)\approx {\frac {2}{\pi }}\operatorname {arctg} [2x(1+x^{4})]} i
erf ( x ) ≈ sgn ( x ) tgh [ 1,152 | x | + 0,064 | x | 4 ] . {\displaystyle \operatorname {erf} (x)\approx \operatorname {sgn}(x)\operatorname {tgh} [1{,}152|x|+0{,}064|x|^{4}].} Są one więc także odwracalne poprzez rozwiązanie zredukowanego równania czwartego i piątego stopnia.
Także bardzo dokładne i odwracalne przybliżenie funkcji błędu (błąd poniżej 0,00035) można uzyskać poprzez deformacje odjęcia funkcji Gaussa od jedynki:
erf ( x ) ≈ sgn ( x ) 1 − e − α ( x ) x 2 , {\displaystyle \operatorname {erf} (x)\approx \operatorname {sgn}(x){\sqrt {1-e^{-\alpha (x)x^{2}}}},} gdzie:
α ( x ) = 4 π + a x 2 1 + a x 2 {\displaystyle \alpha (x)={\frac {{\frac {4}{\pi }}+ax^{2}}{1+ax^{2}}}} jest przybliżeniem Padégo rzędu ( 2 , 2 ) {\displaystyle (2,2)}
a = 8 ( π − 3 ) 3 π ( 4 − π ) ≈ 0,140 012 {\displaystyle a={\frac {8(\pi -3)}{3\pi (4-\pi )}}\approx 0{,}140012} zmieniającej się szerokości funkcji Gaussa.
Przybliżenie to można jeszcze poprawić, redukując błąd do 1 , 5 × 10 − 5 {\displaystyle 1{,}5\times 10^{-5}}
erf ( x ) ≈ sgn ( x ) [ 1 − e − α ( x ) x 2 − 0,002 6 P ( 7 , 13 | x | + 0,000 1 , λ ) ] , {\displaystyle \operatorname {erf} (x)\approx \operatorname {sgn}(x)\left[{\sqrt {1-e^{-\alpha (x)x^{2}}}}-0{,}0026P(7{,}13|x|+0{,}0001,\lambda )\right],} gdzie P ( x ) {\displaystyle P(x)} ( x > 0 ) {\displaystyle (x>0)} wzoru Stirlinga rozkładem Poissona dla λ = 10 , 2 {\displaystyle \lambda =10{,}2}
P ( x , λ ) = e − λ λ x 1 2 π x ( e x ) x . {\displaystyle P(x,\lambda )=e^{-{\lambda }}\lambda ^{x}{\frac {1}{\sqrt {2\pi x}}}\left({\frac {e}{x}}\right)^{x}.}
x erf(x) erfc(x) x erf(x) erfc(x) 0,00 0,0000000 1,0000000 1,30 0,9340079 0,0659921 0,05 0,0563720 0,9436280 1,40 0,9522851 0,0477149 0,10 0,1124629 0,8875371 1,50 0,9661051 0,0338949 0,15 0,1679960 0,8320040 1,60 0,9763484 0,0236516 0,20 0,2227026 0,7772974 1,70 0,9837905 0,0162095 0,25 0,2763264 0,7236736 1,80 0,9890905 0,0109095 0,30 0,3286268 0,6713732 1,90 0,9927904 0,0072096 0,35 0,3793821 0,6206179 2,00 0,9953223 0,0046777 0,40 0,4283924 0,5716076 2,10 0,9970205 0,0029795 0,45 0,4754817 0,5245183 2,20 0,9981372 0,0018628 0,50 0,5204999 0,4795001 2,30 0,9988568 0,0011432 0,55 0,5633234 0,4366766 2,40 0,9993115 0,0006885 0,60 0,6038561 0,3961439 2,50 0,9995930 0,0004070 0,65 0,6420293 0,3579707 2,60 0,9997640 0,0002360 0,70 0,6778012 0,3221988 2,70 0,9998657 0,0001343 0,75 0,7111556 0,2888444 2,80 0,9999250 0,0000750 0,80 0,7421010 0,2578990 2,90 0,9999589 0,0000411 0,85 0,7706681 0,2293319 3,00 0,9999779 0,0000221 0,90 0,7969082 0,2030918 3,10 0,9999884 0,0000116 0,95 0,8208908 0,1791092 3,20 0,9999940 0,0000060 1,00 0,8427008 0,1572992 3,30 0,9999969 0,0000031 1,10 0,8802051 0,1197949 3,40 0,9999985 0,0000015 1,20 0,9103140 0,0896860 3,50 0,9999993 0,0000007
Eric W. E.W. Weisstein Eric W. E.W. , Erf , [w:] MathWorld , Wolfram Research (ang. ) .Probability integral (ang. ) , Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-05-31].GND : 4156112-0 NDL: 00562553 
 Probability integral (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-05-31].
Probability integral (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-05-31].
























![{\displaystyle \operatorname {erf} (x)\approx {\frac {2}{\pi }}\operatorname {arctg} [2x(1+x^{4})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f24afe5b9ac59434e10215cb9a4a5691e7d2bf66)
![{\displaystyle \operatorname {erf} (x)\approx \operatorname {sgn}(x)\operatorname {tgh} [1{,}152|x|+0{,}064|x|^{4}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a9ad8ba275a2c199f26554a8a9441997ab026ac)





![{\displaystyle \operatorname {erf} (x)\approx \operatorname {sgn}(x)\left[{\sqrt {1-e^{-\alpha (x)x^{2}}}}-0{,}0026P(7{,}13|x|+0{,}0001,\lambda )\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c348815570f2725263e4f43a7e59dbc75931656)















